题目内容
13.在△ABC中,角A,B,C的对边分别为a,b,c,sinA,sinB,sinC依次成等比数列,c=2a且$\overrightarrow{BA}$•$\overrightarrow{BC}$=18,则△ABC的面积是3$\sqrt{7}$.分析 根据题意分别求得a和c,b和a的关系,代入余弦定理可求得cosB,进而求得sinB的值,利用已知向量的关系式求得ac,最后代入三角形面积公式即可.
解答 解:依题意知sin2B=sinA•sinC,即b2=ac,
∵c=2a,
∴b=$\sqrt{2}$a,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+4{a}^{2}-2{a}^{2}}{4{a}^{2}}$=$\frac{3}{4}$,
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{7}}{4}$,
∵$\overrightarrow{BA}$•$\overrightarrow{BC}$=c•a•cosB=$\frac{3}{4}$ac=18,
∴ac=24,
∴△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×24×$\frac{\sqrt{7}}{4}$=3$\sqrt{7}$,
故答案为:3$\sqrt{7}$
点评 本题主要考查了正弦定理和余弦定理的应用,向量的数量积的运算.考查了学生的基础知识的综合运用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
18.设F1,F2为椭圆$\frac{x^2}{4}+{y^2}$=1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则$\frac{{|{P{F_2}}|}}{{|{P{F_1}}|}}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
2.已知F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
| A. | $({1,1+\frac{{\sqrt{2}}}{2}})$ | B. | $({1+\frac{{\sqrt{2}}}{2},+∞})$ | C. | $({1,1+\sqrt{2}})$ | D. | $({1+\sqrt{2},+∞})$ |
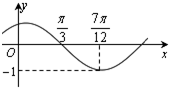 函数f(x)=Acos(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象.
函数f(x)=Acos(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象.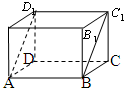 如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.
如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.