题目内容
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)讨论函数![]() 的极值点的个数,并说明理由.
的极值点的个数,并说明理由.
【答案】(1)![]() 或
或![]() .(2)当
.(2)当![]() 时,函数有一个极值点;
时,函数有一个极值点;
当![]() 时,函数无极值点;当
时,函数无极值点;当![]() 时,函数有两个极值点.
时,函数有两个极值点.
【解析】
试题分析:(1)先化简不等式:![]() ,再确定其对于
,再确定其对于![]() 恒成立,而函数
恒成立,而函数![]() 是关于
是关于![]() 的一次函数,因此其等价于
的一次函数,因此其等价于![]() 解一元二次不等式组得
解一元二次不等式组得![]() 的取值范围;(2)因为
的取值范围;(2)因为![]() ,所以先确定导函数零点个数:分两类:一类导函数符号不变,即当
,所以先确定导函数零点个数:分两类:一类导函数符号不变,即当![]() 时,或
时,或![]() 时,第二类:导函数符号有变化:
时,第二类:导函数符号有变化:![]() 且
且![]() 时,或
时,或![]() 时,再确定零点个数,极值点个数
时,再确定零点个数,极值点个数
试题解析:(1)![]() ,
,![]() ,
,
令![]() ,要使
,要使![]() ,则使
,则使![]() 即可,而
即可,而![]() 是关于
是关于![]() 的一次函数,
的一次函数,
∴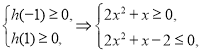 解得
解得![]() 或
或![]() .
.
所以![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(2)令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上递增,无极值点;
上递增,无极值点;
当![]() 时,
时,![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 在
在![]() 上递增,无极值点;
上递增,无极值点;
②当![]() 时,
时,![]() ,设方程
,设方程![]() 的两个根为
的两个根为![]() ,
,![]() (不妨设
(不妨设![]() ),
),
因为![]() ,所以
,所以![]() ,
,![]() ,由
,由![]() ,∴
,∴![]() ,
,
所以当![]() ,
,![]() ,函数
,函数![]() 递增;
递增;
当![]() ,
,![]() ,函数
,函数![]() 递减;
递减;
当![]() ,
,![]() ,函数
,函数![]() 递增;因此函数有两个极值点.
递增;因此函数有两个极值点.
当![]() 时,
时,![]() ,由
,由![]() ,可得
,可得![]() ,
,
所以当![]() ,
,![]() ,函数
,函数![]() 递增;
递增;
当![]() 时,
时,![]() ,函数
,函数![]() 递减;因此函数有一个极值点.
递减;因此函数有一个极值点.
综上,当![]() 时,函数有一个极值点;
时,函数有一个极值点;
当![]() 时,函数无极值点;
时,函数无极值点;
当![]() 时,函数有两个极值点.
时,函数有两个极值点.

练习册系列答案
相关题目


