Question

【题目】如图，已知四棱锥 中，底面 是边长为1的正方形，侧棱 底面 ，且 ， 是侧棱 上的动点.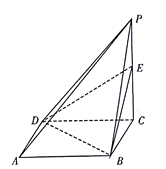

（1）求四棱锥 的表面积；
（2）是否在棱 上存在一点 ，使得 平面 ；若存在，指出点 的位置，并证明；若不存在，请说明理由.

Answer 1

【答案】
（1）解：四棱锥 的底面是边长为1的正方形，侧棱 底面 ，且 ，
∴ ．
∵ ， ，
∴ 平面 ，∴ ，
∴ ．同理， ．
∴
（2）解：当 是 的中点时， 平面 ．

证明：连接 交 于点 ，连接 ，则在三角形 中， 、 分别为 、 的中点，
∴ ，
又∵ 平面 ， 平面 ，
∴ 平面 ．
【解析】(1)首先根据条件确定四棱锥个侧面图形的形状，再根据直角三角形的面积公式以及正方形面积公式代入数值求出表面积。(2)根据题意作出辅助线，由三角形的中位线的性质得到O E / / A P，再根据线面平行的判定定理即可得出结论即可。
【考点精析】解答此题的关键在于理解直线与平面平行的性质的相关知识，掌握一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行．