题目内容
【题目】已知集合A={x|(x+2m)(x﹣m+4)<0},其中m∈R,集合B={x| ![]() >0}.
>0}.
(1)若BA,求实数m的取值范围;
(2)若A∩B=,求实数m的取值范围.
【答案】
(1)解:集合 ![]() ,
,
方法一:(1)当A=时, ![]() ,不符合题意.
,不符合题意.
( 2 )当A≠时, ![]() .
.
①当﹣2m<m﹣4,即 ![]() 时,A={x|﹣2m<x<m﹣4},
时,A={x|﹣2m<x<m﹣4},
又因为BA
所以 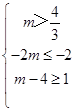 ,即
,即 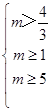 ,所以m≥5;
,所以m≥5;
②当﹣2m>m﹣4,即 ![]() 时,A={x|m﹣4<x<﹣2m}
时,A={x|m﹣4<x<﹣2m}
又因为BA
所以 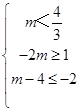 ,即
,即 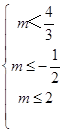 ,所以
,所以 ![]() .
.
综上所述:实数m的取值范围为:m≥5或 ![]() .
.
方法二:因为BA,所以对于x∈B={x|﹣2<x<1},(x+2m)(x﹣m+4)<0恒成立.
令f(x)=(x+2m)(x﹣m+4)则 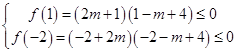
得 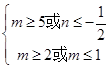 ,
,
所以实数m的取值范围为:m≥5或 ![]()
(2)解:方法一:(1)当A=时, ![]() ,符合题意.
,符合题意.
( 2 )当A≠时, ![]() .
.
①当﹣2m<m﹣4,即 ![]() 时,A={x|﹣2m<x<m﹣4}
时,A={x|﹣2m<x<m﹣4}
又因为A∩B=
所以﹣2m≥1或者 m﹣4≤﹣2,
即 ![]() 或者m≤2,
或者m≤2,
所以 ![]() ;
;
②当﹣2m>m﹣4,即 ![]() 时,A={x|m﹣4<x<﹣2m}
时,A={x|m﹣4<x<﹣2m}
又因为A∩B=
所以m﹣4≥1或者﹣2m≤﹣2,
即m≥5或者m≥1,
所以 ![]()
综上所述:实数m的取值范围为:1≤m≤2.
方法(二)令f(x)=(x+2m)(x﹣m+4)
由A∩B=得
① ![]() 即
即 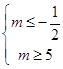 ,所以m∈,
,所以m∈,
② ![]() 即
即 ![]() ,所以1≤m≤2,
,所以1≤m≤2,
综上所述:实数m的取值范围为:1≤m≤2
【解析】(1)化简集合B,方法一、讨论A为空集和不为空集,由集合的包含关系可得m的不等式组,解不等式即可;
方法二、因为BA,所以对于x∈B={x|﹣2<x<1},(x+2m)(x﹣m+4)<0恒成立.可得m的不等式组,解不等式即可;(2)方法一、讨论A为空集和不为空集,结合交集的定义,即可得到所求范围;
方法二、令f(x)=(x+2m)(x﹣m+4),结合交集的定义,可得m的不等式组,解不等式即可得到所求范围.
【考点精析】解答此题的关键在于理解集合的交集运算的相关知识,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.