题目内容
【题目】已知F是抛物线x2=4y的焦点，P是抛物线上的一个动点，且A的坐标为（0，﹣1），则 
的最小值等于 ．
【答案】
【解析】解：由题意可得，抛物线x2=4y的焦点F（0，1），
准线方程为y=﹣1．
过点P作PM垂直于准线，M为垂足，
则由抛物线的定义可得|PF|=|PM|，
则 
= 
=sin∠PAM，∠PAM为锐角；
所以当∠PAM最小时， 最小，
即当PA和抛物线相切时， 最小．
设切点P（2 
，a），由y= 
x2的导数为y′= 
x，
则PA的斜率为k= 2 = = 
，
求得a=1，可得P（2，1），
∴|PM|=2，|PA|=2 
，
∴sin∠PAM= = 
，
则 的最小值等于 ．
所以答案是： ．
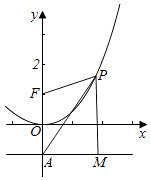
练习册系列答案
相关题目
【题目】随着“全面二孩”政策推行，我市将迎来生育高峰．今年新春伊始，宜城各医院产科就已经是一片忙碌，至今热度不减．卫生部门进行调查统计，期间发现各医院的新生儿中，不少都是“二孩”；在市第一医院，共有40个猴宝宝降生，其中20个是“二孩”宝宝；市妇幼保健院共有30个猴宝宝降生，其中10个是“二孩”宝宝． （I）从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询．
①在市第一医院出生的一孩宝宝中抽取多少个？
②若从7个宝宝中抽取两个宝宝进行体检，求这两个宝宝恰出生不同医院且均属“二孩”的概率；
（Ⅱ）根据以上数据，能否有85%的把握认为一孩或二孩宝宝的出生与医院有关？
附： 
P（k2＞k0） | 0.4 | 0.25 | 0.15 | 0.10 |
k0 | 0.708 | 1.323 | 2.072 | 2.706 |
