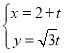题目内容
【题目】已知![]() ,记
,记![]() 为正整数a的各位数字之和。试求正整数t的最小值,使得在任意t个连续的正整数中总能找到一个数c,满足
为正整数a的各位数字之和。试求正整数t的最小值,使得在任意t个连续的正整数中总能找到一个数c,满足![]() 。
。
【答案】见解析
【解析】
设![]() .则
.则
当10![]() (a+1)时,f(a+1)=f(a)+1;
(a+1)时,f(a+1)=f(a)+1;
当![]() 时,
时,
![]() .
.
首先证明:在任意![]() 个连续正整数中,总能找到一个数c,满足m|f(c).
个连续正整数中,总能找到一个数c,满足m|f(c).
若这t个数中有![]() 的倍数,设其为
的倍数,设其为![]() .
.
则f(a)=f(b)=s.
由![]() ,其中,u=0,1,...,8;v=0,1,...,k,知
,其中,u=0,1,...,8;v=0,1,...,k,知![]() 的f值为
的f值为
![]() ,
,
其中,必有一个为9k+r的倍数.
由![]() ,其中,u=0,1,...,9;u=0,1,...,k,知
,其中,u=0,1,...,9;u=0,1,...,k,知![]() 的f值为
的f值为
![]() ,
,
其中,必有一个为9k+r的倍数.
若这t个数中没有![]() 的倍数,则其中有
的倍数,则其中有![]() 的倍数.设最小的倍数为a,f(a)=s.
的倍数.设最小的倍数为a,f(a)=s.
同上,知![]() 的f值为
的f值为![]() ,其中,必有一个为9k+r的倍数.
,其中,必有一个为9k+r的倍数.
综上,在![]() 个连续正整数中必有一数c,满足m|f(c).
个连续正整数中必有一数c,满足m|f(c).
从而,![]() .
.
其次,分三种情形求![]() .
.
1 当r=1,2,4,5,7,8时,![]() .
.
下面构造![]() 个连续正整数,使得其中没有数c,满足mlf(c).
个连续正整数,使得其中没有数c,满足mlf(c).
取![]() ,满足(9k+r)|(9i+1).则在
,满足(9k+r)|(9i+1).则在![]() 中,只有首尾两数的f值是9k+r的倍数.故中间的
中,只有首尾两数的f值是9k+r的倍数.故中间的![]() 个连续正整数中没有数c,满足(9k+r)|f(c).
个连续正整数中没有数c,满足(9k+r)|f(c).
2 当r=3,6时,![]() .
.
因![]() 个连续正整数中必有一数c,满足(9k+r)|f(c).此时,3|f(c).而
个连续正整数中必有一数c,满足(9k+r)|f(c).此时,3|f(c).而![]() 的末尾三数中各自只有一个数是3的倍数,故在连续
的末尾三数中各自只有一个数是3的倍数,故在连续![]() 个数A中首尾共
个数A中首尾共![]() 个数可以去掉,即在
个数可以去掉,即在![]() 个连续正整数中必有一数c,满足(9h+r)|f(c).
个连续正整数中必有一数c,满足(9h+r)|f(c).
下面构造![]() 个连续正整数,使得其中没有数c,满足m|f(c).
个连续正整数,使得其中没有数c,满足m|f(c).
取![]() ,满足(9k+r)|(9i+3),则在
,满足(9k+r)|(9i+3),则在![]() 至
至![]() 这
这![]() 个连续正整数中没有数c,满足(9k+r)|f(c).
个连续正整数中没有数c,满足(9k+r)|f(c).
3 当r=9时,![]() .
.
类似(2)知,9|f(c)且![]() 的末尾九个数中各自只有一个数是9的倍数.
的末尾九个数中各自只有一个数是9的倍数.
故在![]() 个连续正整数中必有一数c,满足9(k+1)|f(c),且在
个连续正整数中必有一数c,满足9(k+1)|f(c),且在
![]() 至
至![]() 这
这![]() 个连续正整数中没有数c,满足9(k+1)|f(c).
个连续正整数中没有数c,满足9(k+1)|f(c).

 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |