题目内容
【题目】有9名学生在同一间教室参加一次数学竞赛,座位排列成3行3列,用![]() 的方格棋盘表示,其中,每个方格代表一个座位为了避免舞弊,采用A、B、C三种类型的试卷,要使任何两个相邻的座位(有公共边的两个方格)发放的试卷类型不同.则符合条件的发放试卷的方法共有________种.
的方格棋盘表示,其中,每个方格代表一个座位为了避免舞弊,采用A、B、C三种类型的试卷,要使任何两个相邻的座位(有公共边的两个方格)发放的试卷类型不同.则符合条件的发放试卷的方法共有________种.
【答案】246
【解析】
用![]() 表示位于第i行第j列的方格,先考虑
表示位于第i行第j列的方格,先考虑![]() 发放A型试卷的方法数.
发放A型试卷的方法数.
令![]() ,
,![]() .
.
考虑M中的格上试卷的类型,有如下几种情形.
(1)都是B型试卷,此时,M中的格上试卷有唯一发放方法,N中的格上试卷都有2种发放方法,共有![]() 种发放方法.
种发放方法.
(2)都是C型试卷,同(1),共有![]() 种发放方法.
种发放方法.
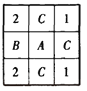
(3)有1格是B型试卷,3格是C型试卷(如图),此时,M中选择一格发放B型试卷,有4种方法,M中其他格上试卷有唯一发放方法,N中的格上试卷都有![]() 种发放方法,共有
种发放方法,共有![]() 种放方法.
种放方法.
(4)有1格是C型试卷,3格是B型试卷,同(3),共有![]() 种发放方法.
种发放方法.
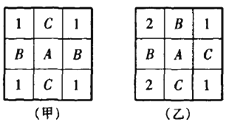
(5)有2格是B型试卷,2格是C型试卷,此时,若2个发放B型试卷的格同行(或列)(如图(甲)),则在M中选择发放B型试卷的格有2种方法,M中其他格上试卷有唯一发放方法,N中的格上试卷只有唯一发放方法,共有2种发放方法;若2个发放B型试卷的格不同行也不同列(如图(乙)),则在M中选择发放B型试卷的格有4种方法,M中其他格上试卷有唯一发放方法,N中的格上试卷有![]() 种发放方法,共有
种发放方法,共有![]() 种发放方法.于是,此种情况共有
种发放方法.于是,此种情况共有![]() 种发放方法.
种发放方法.
由对称性,所有符合要求的发放试卷的方法数为![]() 种.
种.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
