Question

【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”，三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”，用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个大正方形，若直角三角形的直角边的边长分别是3和4，在绘图内随机取一点，则此点取自小正方形的概率为（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

由题意推导出大正方形为长为5，小正方形边长为1，由几何概型概率计算公式得飞镖落在小正方形内的概率．

∵“勾股圆方图”中，四个全等的直角三角形与中间的小正方形拼成一个大正方形，

由已知得到如图：

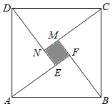
其中AE＝3，则DE＝4，AD5，EF＝1，

现向大正方形内随机投掷一枚飞镖，

则由几何概型概率计算公式得飞镖落在小正方形内的概率是：

，

故选A.