题目内容
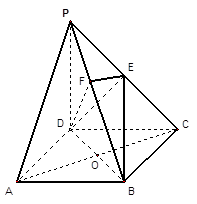
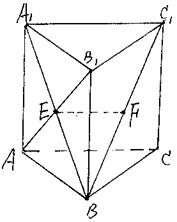
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求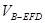 .
.
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求
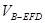 .
.
(1)证明:连结AC,AC交BD于O.连结EO.∵ 底面ABCD是正方形,∴ 点O是AC的中点.在△PAC中,EO是中位线,∴ PA//EO.而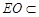 平面EDB,且
平面EDB,且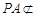 平面EDB,所以,PA//平面EDB.
平面EDB,所以,PA//平面EDB.
(2)证明:∵ PD⊥底面ABCD,且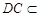 底面ABCD, ∴ PD⊥DC.
底面ABCD, ∴ PD⊥DC.
∵ 底面ABCD是正方形,有DC⊥BC, ∴ BC⊥平面PDC. 而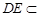 平面PDC,∴ BC⊥DE.又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.
平面PDC,∴ BC⊥DE.又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.
而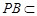 平面PBC,∴ DE⊥PB.又EF⊥PB,且
平面PBC,∴ DE⊥PB.又EF⊥PB,且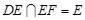 ,所以PB⊥平面EFD.
,所以PB⊥平面EFD.
(3)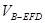 =
=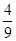
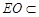 平面EDB,且
平面EDB,且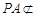 平面EDB,所以,PA//平面EDB.
平面EDB,所以,PA//平面EDB. (2)证明:∵ PD⊥底面ABCD,且
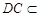 底面ABCD, ∴ PD⊥DC.
底面ABCD, ∴ PD⊥DC. ∵ 底面ABCD是正方形,有DC⊥BC, ∴ BC⊥平面PDC. 而
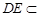 平面PDC,∴ BC⊥DE.又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.
平面PDC,∴ BC⊥DE.又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.而
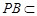 平面PBC,∴ DE⊥PB.又EF⊥PB,且
平面PBC,∴ DE⊥PB.又EF⊥PB,且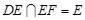 ,所以PB⊥平面EFD.
,所以PB⊥平面EFD. (3)
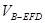 =
=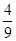
略

练习册系列答案
相关题目
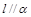 ,
,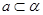 ,则
,则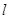 与
与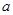 的位置关系一定是( )
的位置关系一定是( )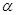 没有公共点
没有公共点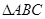 是等腰直角三角形,
是等腰直角三角形,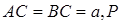 是
是 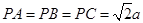
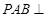 面
面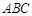 ;
;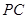 和
和
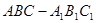 中,
中,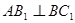 ,
,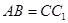
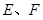 分别为
分别为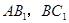 的中点
的中点

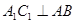
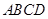 各边
各边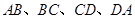 上分别取
上分别取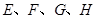 四点,如果与
四点,如果与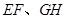 能相交于点
能相交于点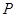 ,那么
,那么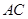 上
上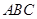 内
内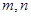 为直线,
为直线,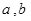 为平面,给出下列结论:
为平面,给出下列结论: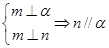 ②
②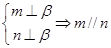 ③
③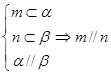 ④
④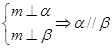
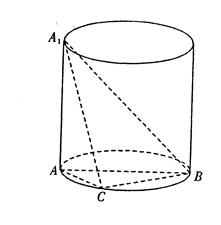
 面ABC,高为5,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为_______
面ABC,高为5,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为_______