Question

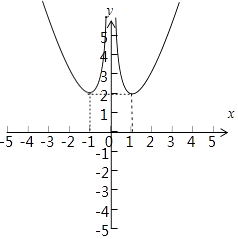
【题目】已知函数f（x）=2x+2﹣x ． （Ⅰ）试写出这个函数的性质（不少于3条，不必说明理由），并作出图象；
（Ⅱ）设函数g（x）=4x+4﹣x﹣af（x），求这个函数的最小值．

Answer 1

【答案】解：（Ⅰ）偶函数；定义域R；值域{y|y≥2}； 单调递增区间：（0，+∞），单调递减区间：（﹣∞，0）等
图象如图：．
（Ⅱ）设2x+2﹣x=t（t≥2），则4x+4﹣x=t2﹣2，设k（t）=t2﹣2﹣at=t2﹣at﹣2，
时，k（t）min=k（2）=2﹣2a；
时 ．
所以， 时，g（x）min=2﹣2a；
时 ．

【解析】（Ⅰ）列出函数的偶函数；定义域R；值域；单调递增区间，单调递减区间，选择3项即可，画出图象．（Ⅱ）设2x+2﹣x=t（t≥2），则4x+4﹣x=t2﹣2，设k（t）=t2﹣2﹣at=t2﹣at﹣2，通过a与2讨论，利用二次函数的最值求解即可．
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．