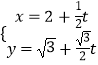题目内容
【题目】设f(a)＝|x2－a2|dx
（1）当0≤a≤1与a＞1时，分别求f(a)；
（2）当a≥0时，求f(a)的最小值．
【答案】
（1）
【解答】
当0≤a≤1时，
当a>1时，
所以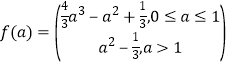
（2）
【解答】
当a>1时，由于
在
上是增函数，
故f(a)在上的最小值是
,
当
时，f'(a)=4a2-2a=2a(2a-1),
由f(a)>0知，
或a<0,
故f(a)在
上递减 ，在
上递增，
因此在[0,1]上，f(a)的最小值为
,
综上可知，f(a)在
上的最小值为
.
【解析】因为f(a)＝|x2－a2|dx中带有绝对值，在计算的过程中首先要分类讨论去掉绝对值，本题考查了分类讨论求解问题的能力，难度较大
【考点精析】解答此题的关键在于理解定积分的概念的相关知识，掌握定积分的值是一个常数，可正、可负、可为零；用定义求定积分的四个基本步骤：①分割；②近似代替；③求和；④取极限．
练习册系列答案
相关题目
