题目内容
【题目】如图,在矩形![]() 中
中![]() ,E为
,E为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,
的位置,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列结论正确的是( )
的中点,则在翻折过程中,下列结论正确的是( )
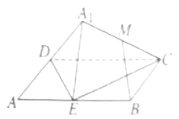
A.恒有![]() 平面
平面![]()
B.B与M两点间距离恒为定值
C.三棱锥![]() 的体积的最大值为
的体积的最大值为![]()
D.存在某个位置,使得平面![]() ⊥平面
⊥平面![]()
【答案】ABC
【解析】
对每一个选项逐一分析研究得解.
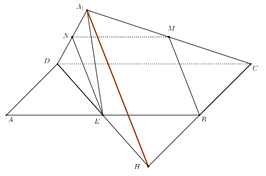
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,可得四边形
,可得四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,所以
,所以![]() 平面
平面![]() ,故A正确;
,故A正确;
(也可以延长![]() 交于
交于![]() ,可证明
,可证明![]() ,从而证明
,从而证明![]() 平面
平面![]() )
)
因为![]() ,
,![]() ,
,![]() ,
,
根据余弦定理得
![]() ,
,
得![]() ,
,
因为![]() ,故
,故![]() ,故B正确;
,故B正确;
因为![]() 为
为![]() 的中点,
的中点,
所以三棱锥![]() 的体积是三棱锥
的体积是三棱锥![]() 的体积的两倍,
的体积的两倍,
故三棱锥![]() 的体积
的体积![]() ,其中
,其中![]() 表示
表示![]() 到底面
到底面![]() 的距离,当平面
的距离,当平面![]() 平面
平面![]() 时,
时,![]() 达到最大值,
达到最大值,
此时![]() 取到最大值
取到最大值![]() ,所以三棱锥
,所以三棱锥![]() 体积的最大值为
体积的最大值为![]() ,故C正确;
,故C正确;
考察D选项,假设平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
故![]() 平面
平面![]() ,所以
,所以![]() ,
,
则在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() ,故
,故![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
所以![]() ,得
,得![]() 平面
平面![]() ,与题干条件
,与题干条件![]() 平面
平面![]() 矛盾,故D不正确;
矛盾,故D不正确;
故选:A,B,C.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
