Question

【题目】已知函数 ，若函数的图象与轴的交点个数不少于2个，则实数的取值范围是（ ）

A. B.

C. D.

Answer 1

【答案】C

【解析】分析：根据的图象与轴的交点个数不少于2个，可得函数的图象与的交点个数不少于2个，在同一坐标系中画出两个函数图象，结合图象即可得到m的取值范围.

详解： 的图象与轴的交点个数不少于2个，

函数的图象与函数的图象的交点个数不少于2个，

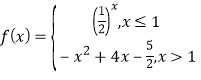函数，

时，函数为指数函数，过点，

时，函数，为对称轴，开口向下的二次函数.

，

为过定点的一条直线.

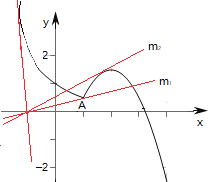
在同一坐标系中，画出两函数图象，如图所示.

（1）当时，

①当过点时，两函数图象有两个交点，

将点代入直线方程，解得.

②当与相切时，两函数图象有两个交点.

联立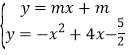，整理得

则，解得，（舍）

如图当，两函数图象的交点个数不少于2个.

（2）当时，易得直线与函数必有一个交点

如图当直线与相切时有另一个交点

设切点为，

，

切线的斜率， 切线方程为

切线与直线重合，即点在切线上.

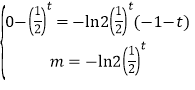，解得

由图可知，当,两函数图象的交点个数不少于2个.

综上，实数的取值范围是

故选C.