题目内容
若函数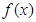 是定义在
是定义在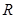 上的偶函数,在
上的偶函数,在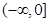 上是增函数,且
上是增函数,且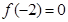 ,则使得
,则使得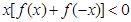 的
的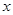 的取值范围是_______.
的取值范围是_______.
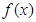 是定义在
是定义在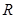 上的偶函数,在
上的偶函数,在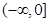 上是增函数,且
上是增函数,且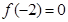 ,则使得
,则使得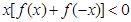 的
的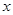 的取值范围是_______.
的取值范围是_______.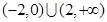
试题分析:因为
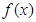 在
在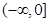 上是增函数,且
上是增函数,且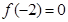 ,所以当
,所以当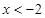 时,
时,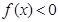 ,
,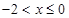 时,
时,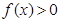 ,又因为函数
,又因为函数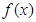 是定义在
是定义在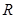 上的偶函数,所以
上的偶函数,所以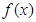 的图像关于
的图像关于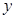 轴对称,所以当
轴对称,所以当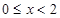 时,
时,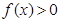 ,
,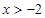 时,
时,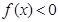 ,所以不等式
,所以不等式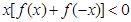 即
即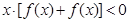 也就是
也就是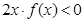
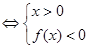 或
或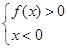 ,解得
,解得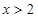 或
或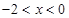 ,故不等式
,故不等式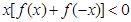 的解集为
的解集为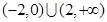 .
.
练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
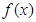 是定义在
是定义在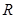 上的偶函数,在
上的偶函数,在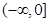 上是增函数,且
上是增函数,且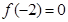 ,则使得
,则使得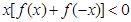 的
的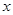 的取值范围是_______.
的取值范围是_______.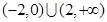
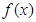 在
在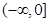 上是增函数,且
上是增函数,且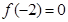 ,所以当
,所以当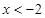 时,
时,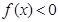 ,
,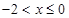 时,
时,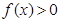 ,又因为函数
,又因为函数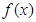 是定义在
是定义在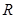 上的偶函数,所以
上的偶函数,所以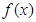 的图像关于
的图像关于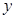 轴对称,所以当
轴对称,所以当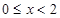 时,
时,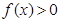 ,
,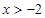 时,
时,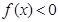 ,所以不等式
,所以不等式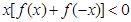 即
即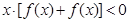 也就是
也就是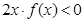
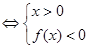 或
或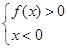 ,解得
,解得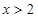 或
或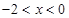 ,故不等式
,故不等式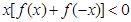 的解集为
的解集为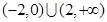 .
.
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案