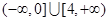题目内容
已知常数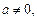 数列
数列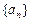 的前
的前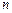 项和为
项和为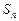 ,
,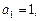 且
且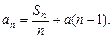
(1)求证:数列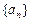 为等差数列;
为等差数列;
(2)若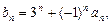 且数列
且数列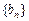 是单调递增数列,求实数
是单调递增数列,求实数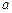 的取值范围;
的取值范围;
(3)若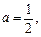 数列
数列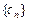 满足:
满足: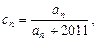 对于任意给定的正整数
对于任意给定的正整数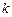 ,是否存在
,是否存在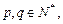 使
使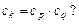 若存在,求
若存在,求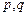 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.
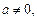 数列
数列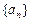 的前
的前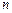 项和为
项和为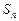 ,
,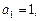 且
且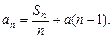
(1)求证:数列
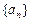 为等差数列;
为等差数列;(2)若
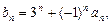 且数列
且数列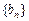 是单调递增数列,求实数
是单调递增数列,求实数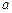 的取值范围;
的取值范围;(3)若
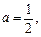 数列
数列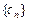 满足:
满足: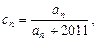 对于任意给定的正整数
对于任意给定的正整数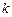 ,是否存在
,是否存在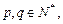 使
使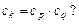 若存在,求
若存在,求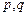 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.(Ⅰ)∵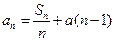 ∴
∴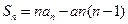 ,
,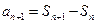 , ┄┄┄2分
, ┄┄┄2分
∴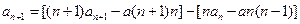
化简得: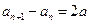 (常数),
(常数),
∴数列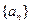 是以1为首项,公差为
是以1为首项,公差为 的等差数列; ┄┄┄4分
的等差数列; ┄┄┄4分
(Ⅱ)由(Ⅰ)知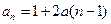 ,又∵
,又∵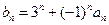 ,
,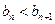 ,
,
∴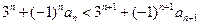 ,∴
,∴
①当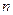 是奇数时,∵
是奇数时,∵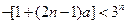 ,∴
,∴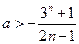 ,
,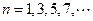
令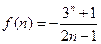 ,∴
,∴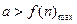
∵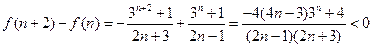
∴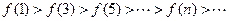 ,且
,且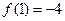 ,∴
,∴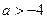 ; ┄7分
; ┄7分
②当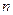 是偶数时,∵
是偶数时,∵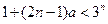 ,∴
,∴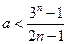 ,
,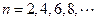
令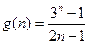 ,∴
,∴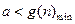
∵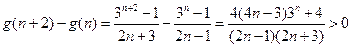
∴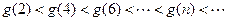 ,且
,且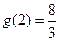 ,∴
,∴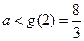 ;
;
综上可得:实数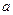 的取值范围是
的取值范围是 . ┄10分
. ┄10分
(Ⅲ)由(Ⅰ)知, ,又∵
,又∵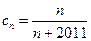 ,
,
设对任意正整数k,都存在正整数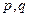 ,使
,使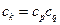 ,
,
∴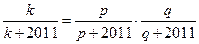 ,∴
,∴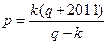 ┄┄┄12分
┄┄┄12分
令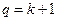 ,则
,则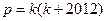 (或
(或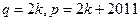 )
)
∴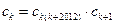 (或
(或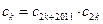 ) ┄16分
) ┄16分
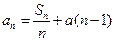 ∴
∴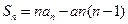 ,
,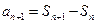 , ┄┄┄2分
, ┄┄┄2分∴
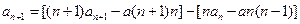
化简得:
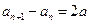 (常数),
(常数), ∴数列
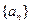 是以1为首项,公差为
是以1为首项,公差为 的等差数列; ┄┄┄4分
的等差数列; ┄┄┄4分(Ⅱ)由(Ⅰ)知
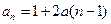 ,又∵
,又∵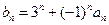 ,
,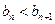 ,
,∴
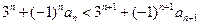 ,∴
,∴
①当
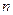 是奇数时,∵
是奇数时,∵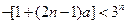 ,∴
,∴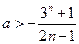 ,
,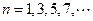
令
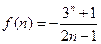 ,∴
,∴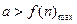
∵
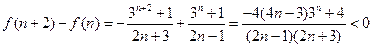
∴
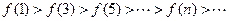 ,且
,且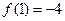 ,∴
,∴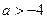 ; ┄7分
; ┄7分②当
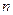 是偶数时,∵
是偶数时,∵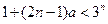 ,∴
,∴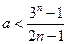 ,
,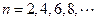
令
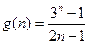 ,∴
,∴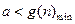
∵
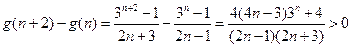
∴
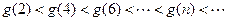 ,且
,且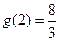 ,∴
,∴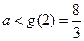 ;
;综上可得:实数
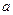 的取值范围是
的取值范围是 . ┄10分
. ┄10分(Ⅲ)由(Ⅰ)知,
 ,又∵
,又∵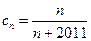 ,
,设对任意正整数k,都存在正整数
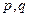 ,使
,使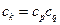 ,
,∴
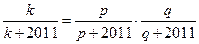 ,∴
,∴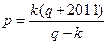 ┄┄┄12分
┄┄┄12分令
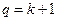 ,则
,则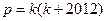 (或
(或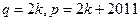 )
)∴
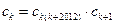 (或
(或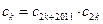 ) ┄16分
) ┄16分略

练习册系列答案
相关题目
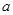 元(一年定期),若年利率为
元(一年定期),若年利率为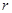 保持不变,且每年到期存款自动转为新的一年定期,到2012年1月1日将所有存款及利息全部取回,他可取回的钱数为( )(单位为元)
保持不变,且每年到期存款自动转为新的一年定期,到2012年1月1日将所有存款及利息全部取回,他可取回的钱数为( )(单位为元)



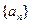 和
和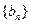 中,数列
中,数列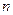 项和记为
项和记为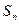 . 若点
. 若点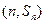 在函数
在函数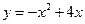 的图象上,点
的图象上,点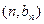 在函数
在函数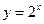 的图象上。
的图象上。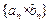 的前
的前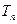
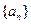 中
中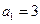 ,
,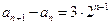
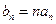 ,求数列
,求数列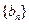 的前
的前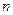 项和
项和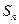
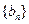 满足
满足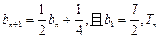 为
为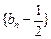 是等比数列,并求
是等比数列,并求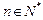 ,不等式
,不等式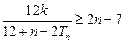 恒成立,求实数
恒成立,求实数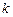 的取值范围.
的取值范围.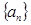 的前n项和为Sn ,若
的前n项和为Sn ,若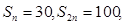 则
则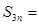 ( )
( )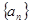 中
中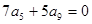 ,且
,且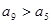 ,则使前
,则使前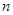 项和
项和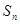 取最小值
取最小值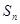 为等差数列
为等差数列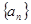 的前
的前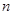 项的和,
项的和,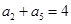 ,
,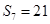 ,则
,则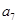 的值为( )
的值为( )
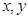 为正实数,且
为正实数,且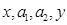 成等差数列,
成等差数列,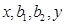 成等比数列,则
成等比数列,则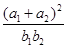 的取值范围是 ( )
的取值范围是 ( )