题目内容
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() =
=![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
⑴当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数![]() 的取值范围;
的取值范围;
(3)若对于任意实数![]() ,函数
,函数![]() 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)f(x)的不动点为-1,2;(2)-4<b<4或4<b<6;(3)0<a<2.
【解析】试题分析:本题为新定义信息题,把a=2,b=-2代入后得到函数f(x)的解析式,假设存在不动点,根据不动点定义,满足![]() ,解方程求出不动点;当
,解方程求出不动点;当![]() 时,函数
时,函数![]() 在
在![]() 内有两个不同的不动点,说明方程在区间(-2,3)内有两个不等式实数根;同理解决第三步.
内有两个不同的不动点,说明方程在区间(-2,3)内有两个不等式实数根;同理解决第三步.
试题解析:
(1)当a=2,b=-2时,f(x)=2x2-x-4
∴ 由f(x)=x得x2-x-2=0, ∴ x=-1或x=2.
∴ f(x)的不动点为-1,2.
(2) 当a=2时,f(x)=2x2+(b+1)x+b-2,
由题意得f(x)=x在(-2,3)内有两个不同的不动点,
即方程 2x2+bx+b-2=0 在(-2,3)内的两个不相等的实数根.
设 g(x)=2x2+bx+b-2,
∴ 只须满足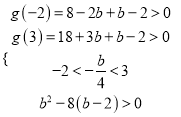 ∴
∴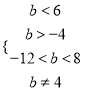
∴ -4<b<4或4<b<6
(3)由题意得:对于任意实数b,方程 ax2+bx+b-2=0总有两个不相等的实数解.
∴ ![]() ∴ b2-4ab+8a>0对b∈R恒成立.
∴ b2-4ab+8a>0对b∈R恒成立.
∴16a2-32a<0 ∴ 0<a<2.

练习册系列答案
相关题目