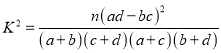题目内容
【题目】.已知函数f(x)=x2-2x-3,若x∈[t,t+2]时,求函数f(x)的最值.
【答案】详见解析.
【解析】试题分析:二次函数的对称轴是x=1,分类讨论对称轴在区间左边,对称轴在区间右边以及对称轴在区间内三类讨论,按照函数的单调性求出最值,当对称轴在区间内时,再分成对称轴在区间中点左边和右边两类求最大值,最后写成分段函数的形式.
试题解析:
∵对称轴x=1,
(1)当1≥t+2,即t≤-1时,f(x)max=f(t)=t2-2t-3,f(x)min=f(t+2)=t2+2t-3.
(2)当![]() ≤1<t+2,即-1<t≤0时,f(x)max=f(t)=t2-2t-3,f(x)min=f(1)=-4.
≤1<t+2,即-1<t≤0时,f(x)max=f(t)=t2-2t-3,f(x)min=f(1)=-4.
(3)当t≤1<![]() ,即0<t≤1时,f(x)max=f(t+2)=t2+2t-3,f(x)min=f(1)=-4.
,即0<t≤1时,f(x)max=f(t+2)=t2+2t-3,f(x)min=f(1)=-4.
(4)当1<t,即t>1时,f(x)max=f(t+2)=t2+2t-3,f(x)min=f(t)=t2-2t-3.
设函数最大值为g(t),最小值为φ(t)时,则有
g(t)=![]() φ(t)=
φ(t)=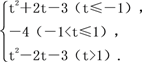
点睛:本题考查二次函数的最值问题,体现了分类讨论思想,属于中档题.由题意二次函数的开口向上,且对称轴为x=1,故讨论对称轴与区间端点t和t+2的大小关系,当对称轴大于等于t+2时,函数单调递减;当对称轴小于t时,函数单调递增;当对称轴在区间内时,函数先减后增,在对称轴处取最小值,再比较1与两端点中点的大小,当1大于等于中点时,在x=t处取最大值, 当1小于中点时,在x=t+2处取最大值.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |