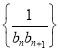题目内容
【题目】【2014山东.理15】已知函数![]() ,对函数
,对函数![]() ,定义
,定义![]() 关于
关于![]() 的对称函数为函数
的对称函数为函数![]() ,
,![]() 满足:对于任意
满足:对于任意![]() ,两个点
,两个点![]() 关于点
关于点![]() 对称,若
对称,若![]() 是
是![]() 关于
关于![]() 的“对称函数”,且
的“对称函数”,且![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】由“对称函数”的定义及中点坐标公式得![]() 所以,
所以,![]() ,
,![]() 恒成立即
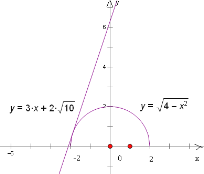
恒成立即![]() 恒成立,亦即直线
恒成立,亦即直线![]() 位于半圆
位于半圆![]() 的上方.在同一坐标系内,画出直线
的上方.在同一坐标系内,画出直线![]() 及半圆
及半圆![]() (如图所示),当直线与半圆相切时,
(如图所示),当直线与半圆相切时,![]() 解得
解得![]() ,故答案为
,故答案为![]()
【思路点拨】本题考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系.解答本题的关键,是理解新定义运算,将问题转化成![]() 恒成立,利用数形结合思想,再将问题转化成直线与圆的位置关系问题.本题属于新定义问题,是一道创新能力题,中等难度之上.在考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系等的同时,考查转化与化归思想及数形结合思想.
恒成立,利用数形结合思想,再将问题转化成直线与圆的位置关系问题.本题属于新定义问题,是一道创新能力题,中等难度之上.在考查阅读理解能力、学习能力、运算能力、直线与圆的位置关系等的同时,考查转化与化归思想及数形结合思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目