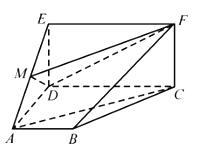
题目内容
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() 是抛物线
是抛物线![]() 上不同两点,且
上不同两点,且![]() (其中
(其中![]() 是坐标原点),直线
是坐标原点),直线![]() 与
与![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求抛物线![]() 的准线方程;
的准线方程;
(Ⅱ)求证:直线![]() 与
与![]() 轴平行.
轴平行.
【答案】(1) ![]() .(2)见解析.
.(2)见解析.
【解析】
(Ⅰ)把点代入即可求出p的值,可得抛物线C的准线方程,
(Ⅱ)由题意可设直线AB的方程为y=x+m,设A(x1,y1),B(x2,y2),由题意可得y1+y2=2,即可求出点Q的纵坐标,再分别求出直线OA,BM的方程,求出点P的纵坐标,即可证明.
(Ⅰ)由题意得![]() ,解得
,解得![]() .
.
所以抛物线![]() 的准线方程为
的准线方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
由![]() 得
得![]() ,则
,则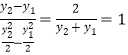 ,所以
,所以![]() .
.
所以线段![]() 中点
中点![]() 的为纵坐标
的为纵坐标![]() .
.
直线![]() 方程为
方程为 ┅①
┅①
直线![]() 方程为
方程为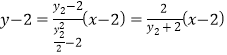 ┅②
┅②
联立①②解得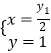 ,即点
,即点![]() 的为纵坐标
的为纵坐标![]() .
.
如果直线![]() 斜率不存在,结论也显然成立.
斜率不存在,结论也显然成立.


【题目】为了打好“精准扶贫攻坚战”某村扶贫书记打算带领该村农民种植新品种蔬菜,可选择的种植量有三种:大量种植,适量种植,少量种植.根据收集到的市场信息,得到该地区该品种蔬菜年销量频率分布直方图如图,然后,该扶贫书记同时调查了同类其他地区农民以往在各种情况下的平均收入如表1(表中收入单位:万元):
表1
销量 种植量 | 好 | 中 | 差 |
大量 |
| 8 | -4 |
适量 | 9 | 7 | 0 |
少量 | 4 | 4 | 2 |
但表格中有一格数据被墨迹污损,好在当时调查的数据频数分布表还在,其中大量种植的100户农民在市场销量好的情况下收入情况如表2:
收入(万元) | 11 | 11.5 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
频数(户) | 5 | 10 | 15 | 10 | 15 | 20 | 10 | 10 | 5 |
(Ⅰ)根据题中所给数据,请估计在市场销量好的情况下,大量种植的农民每户的预期收益.(用以往平均收入来估计);
(Ⅱ)若该地区年销量在10千吨以下表示销量差,在10千吨至30千吨之间表示销量中,在30千吨以上表示销量好,试根据频率分布直方图计算销量分别为好、中、差的概率(以频率代替概率);
(Ⅲ)如果你是这位扶贫书记,请根据(Ⅰ)(Ⅱ),从农民预期收益的角度分析,你应该选择哪一种种植量.