题目内容
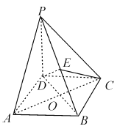
【题目】已知点
是单位正方体
的对角面
上的一动点，过点作垂直于平面的直线，与正方体的侧面相交于
、
两点，则
的面积的最大值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
根据题意和正方体的特征，分析点P动的过程中，x随着y变化情况作出轨迹图象，数形结合能求出结果．
解：由题意知，MN⊥平面BB1D1D，其轨迹经过B，D1和侧棱AA1，CC1的中点E，F，
如图，设正方体中心为O1,当P点在线段BO1上运动时，MN随BP的增大而线性增大，所以△BMN的面积表达式应是开口向上的二次函数图像递增的一部分; 当P点在线段D1O1上运动时, MN随D1P的增大而线性减小，所以△BMN的面积表达式应是开口向下的二次函数图像递减的一部分.所以当MN与EF重合时，△BMN的面积取最大值，
此时，BM＝BN
，
MN
，
S△BMN
．
故选：A．
练习册系列答案
相关题目
