题目内容
【题目】已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+![]() t≤t2,求实数t的取值范围.
t≤t2,求实数t的取值范围.
【答案】(Ⅰ)见解析. (Ⅱ)![]() .
.
【解析】
(Ⅰ)利用a1+a2+a3+…+an=n﹣an,再写一式,两式相减,整理可得数列{an-1}是等比数列;(Ⅱ)先确定bn![]() ,再利用bn+1﹣bn,确定bn有最大值b3=b4
,再利用bn+1﹣bn,确定bn有最大值b3=b4![]() ,从而对任意n∈N*,都有bn
,从而对任意n∈N*,都有bn![]() t≤t2,等价于对任意n∈N*,都有
t≤t2,等价于对任意n∈N*,都有![]() t2
t2![]() t成立,由此可求实数t的取值范围.
t成立,由此可求实数t的取值范围.
(Ⅰ)由题可知:![]() ,①
,①
![]() ,②
,②
②-①可得![]() .
.
即:![]() ,又
,又![]() .
.
所以数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)可得![]() ,
,
∴![]() .
.
由![]() 可得
可得![]() ,
,
由![]() 可得
可得![]() .
.
所以![]() ,
,![]() ,
,
故![]() 有最大值
有最大值![]() .
.
所以,对任意![]() ,都有
,都有![]() ,等价于对任意
,等价于对任意![]() ,都有
,都有![]() 成立.
成立.
所以![]() ,
,
解得![]() 或
或![]() .
.
所以,实数![]() 的取值范围是
的取值范围是![]() .
.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】甲、乙两名大学生因为学习需要,欲各自选购一台笔记本电脑,他们决定在A,B,C三个品牌的五款产品中选择,这五款笔记本电脑在某电商平台的价格与销量数据如表所示:
品牌 | A | B | C | ||
型号 | A﹣1 | A﹣2 | B﹣1 | B﹣2 | C﹣1 |
价格(元) | 6000 | 7500 | 10000 | 8000 | 4500 |
销量(台) | 1000 | 1000 | 200 | 800 | 3000 |
(Ⅰ)若甲选择某品牌的笔记本电脑的概率与该品牌的总销量成正比,求他选择B品牌的笔记本电脑的概率;
(Ⅱ)若甲、乙两人选择每种型号的笔记本电脑的概率都相等,且两人选购的型号不相同,求他们两人购买的笔记本电脑的价格之和大于15000元的概率.
【题目】为了了解高一学生的心理健康状况,某校心理健康咨询中心对该校高一学生的睡眠状况进行了抽样调查.该中心随机抽取了60名高一男生和40名高一女生,统计了他们入学第一个月的平均每天睡眠时间,得到如下频数分布表.规定:“平均每天睡眠时间大于等于8小时”为“睡眠充足”,“平均每天睡眠时间小于8小时”为“睡眠不足”.
高一男生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 3 | 20 | 19 | 10 | 8 |
高一女生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 20 | 11 | 5 | 2 |
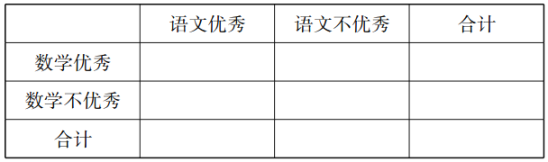
(1)请将下面的列联表补充完整,并根据已完成的![]() 列联表,判断是否有
列联表,判断是否有![]() 的把握认为“睡眠是否充足与性别有关”?
的把握认为“睡眠是否充足与性别有关”?
睡眠充足 | 睡眠不足 | 合计 | |
男生 | 42 | ||
女生 | 7 | ||
合计 | 100 |
(2)由样本估计总体的思想,根据这两个频数分布表估计该校全体高一学生入学第一个月的平均每天睡眠时间(同一组中的数据以这组数据所在区间中点的值作代表);
(3)若再从这100人中平均每天睡眠时间不足6小时的同学里随机抽取两人进行心理健康干预,则抽取的两人中包含女生的概率是多少?
附:参考公式:![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |