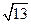题目内容
设 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与曲线
与曲线 的距离.
的距离.
(1)求曲线 与直线
与直线 的距离;
的距离;
(2)设曲线 与直线
与直线 (
( )的距离为
)的距离为 ,直线
,直线 与直线
与直线 的距离为
的距离为 ,求
,求 的最小值.
的最小值.
 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与曲线
与曲线 的距离.
的距离.(1)求曲线
 与直线
与直线 的距离;
的距离;(2)设曲线
 与直线
与直线 (
( )的距离为
)的距离为 ,直线
,直线 与直线
与直线 的距离为
的距离为 ,求
,求 的最小值.
的最小值.(1)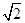 ;(2)
;(2)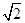 .
.
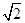 ;(2)
;(2)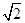 .
.试题分析:(1)曲线
 上任意一点点
上任意一点点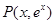 到
到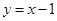 的距离为
的距离为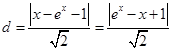 ,用求导的方法判断最小值;(2)根据题意,
,用求导的方法判断最小值;(2)根据题意,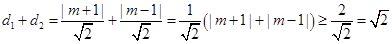 ,应用基本不等式求出最小值,注意一正二定三相等.
,应用基本不等式求出最小值,注意一正二定三相等.试题解析:(1)只需求曲线
 上的点到直线
上的点到直线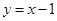 距离的最小值. 1分
距离的最小值. 1分设曲线
 上任意一点为
上任意一点为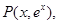 则点
则点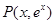 到
到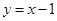 的距离为
的距离为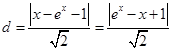 3分
3分令
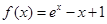 ,则
,则 ,由
,由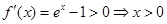 ;
; 5分
5分故当
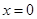 时, 函数
时, 函数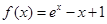 取极小值即最小值
取极小值即最小值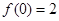 ,
,即
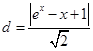 取最小值
取最小值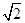 ,故曲线
,故曲线 与曲线
与曲线 的距离为
的距离为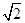 ; 8分
; 8分(2)由(1)可知,
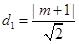 ,又易知
,又易知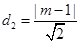 , 9分
, 9分则
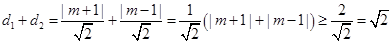 , 12分
, 12分当且仅当
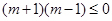 时等号成立,考虑到
时等号成立,考虑到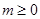 ,所以,当
,所以,当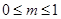 时,
时, 的最小值为
的最小值为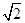 . 14分
. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

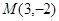 ,
,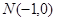 ,则线段
,则线段 的中点
的中点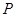 的坐标是________.
的坐标是________.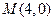 ,
,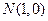 ,若动点
,若动点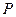 满足
满足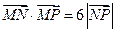 ,
,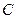 .
.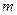 的取值范围,使得对于直线
的取值范围,使得对于直线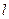 :
: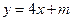 ,曲线
,曲线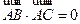 ,
, 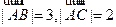 ,则
,则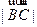 =( )
=( ) 
 B.
B. 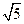 C.
C. 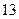 D.
D.