题目内容
9.已知命题p:若a>0,b>0,a+b=4,则$\frac{1}{a}+\frac{1}{b}$的最小值为1;命题q:函数y=ln(x+$\sqrt{1+{x}^{2}}$)是奇函数.判断命题“p∧q”“p∨q”的真假.分析 根据基本不等式的性质判断出p的真假,再根据对数函数的性质判断出q的真假,从而判断出复合命题的真假.
解答 解:关于命题p:若a>0,b>0,a+b=4,
则$\frac{a}{4}$+$\frac{b}{4}$=1,
∴($\frac{1}{a}+\frac{1}{b}$)($\frac{a}{4}$+$\frac{b}{4}$)=$\frac{1}{2}$+$\frac{b}{4a}$+$\frac{a}{4b}$≥$\frac{1}{2}$+2$\sqrt{\frac{b}{4a}•\frac{a}{4b}}$=1
当且仅当a=b=2时“=”成立,
命题p是真命题;
关于命题q:函数y=ln(x+$\sqrt{1+{x}^{2}}$)不是奇函数,
命题q是假命题,
∴“p∧q”是假命题,“p∨q”是真命题.
点评 本题考查了复合命题的判断,考查基本不等式的性质,对数函数的性质,是一道基础题.

练习册系列答案
相关题目
20.“$θ∈(\frac{π}{2},π)$”是“sinθ-cosθ>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
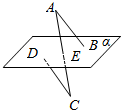 如图,已知AB∥CD,AB∩α=B,CD∩α=D,AC∩α=E,求证:E,B,D三点共线.
如图,已知AB∥CD,AB∩α=B,CD∩α=D,AC∩α=E,求证:E,B,D三点共线.