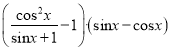Question

【题目】已知函数，关于的不等式只有1个整数解，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】由得。

∴当时， 单调递增；当时， 单调递减。

∴当时， 有最大值，且，

且x→+∞时，f(x)→0；x→0时，x→∞；f(1)=0。

故在(0,1)上， ，在(1,+∞)上， ，

作出函数f(x)的图象如下：

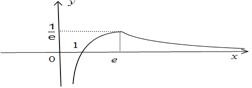
①当时，由得，解集为(0,1)∪(1,+∞)，

所以不等式的整数解有无数多个，不合题意；

②当时，由得或。

当时，解集为(1,+∞)，有无数个整数解；

当时，解集为(0,1)的子集，不含有整数解。

故不合题意。

③当时，由得或，

当时，解集为(0,1)，不含有整数解；

当时，由条件知只有一个整数解。

∵在上单调递增，在上单调递减，

而，

∴满足条件的整数解只能为3，

∴，

∴。

综上，选D。