题目内容
【题目】已知等差数列{
}的前n项和为Sn，公差d＞0，且
， 
,公比为q（0＜q＜1）的等比数列{
}中， 
（1）求数列{
}，{
}的通项公式
， 
；
（2）若数列{
}满足
，求数列{
}的前n项和Tn。
【答案】（1）
（2）
为正偶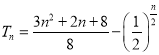数时, 
； 
为正奇数时，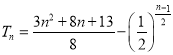 
【解析】试题分析：（1）由
，列出关于首项
、公差
的方程组，解方程组可得
与
的值，从而可得数列
的通项公式，公比为
的等比数列
中， 
，可得
，利用等比数列的定义，求出公比，从而可得{
}的通项公式；（2）由
，对
分类讨论，利用分组求和法根据等差数列与等比数列的前
项公式即可得结果.
试题解析：（1）因为
为等差数列，所以
又
又公差
,所以
所以
所以
解得
所以
因为公比为
的等比数列
中， 
所以，当且仅当
时成立.
此时公比
所以
（2）①
为正偶数时, 
的前
项和
中, 
， 
各有前
项,由（1）知
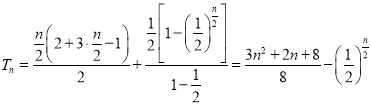
②
为正奇数时, 
中, 
， 
分别有前
项、
项.
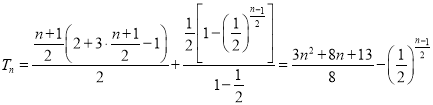
【方法点晴】本题主要考查等差数列及等比数列的通项、等差数列及等比数列的求和公式以及利用“分组求和法”求数列前
项和，属于中档题. 利用“分组求和法”求数列前
项和常见类型有两种：一是通项为两个公比不相等的等比数列的和或差，可以分别用等比数列求和后再相加减；二是通项为一个等差数列和一个等比数列的和或差，可以分别用等差数列求和、等比数列求和后再相加减.
练习册系列答案
相关题目
