题目内容
15.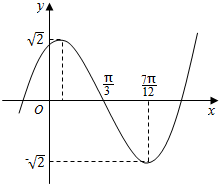 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
分析 根据已知函数的图象,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将($\frac{π}{3}$,0)代入解析式,可求出φ值,进而求出函数的解析式.
解答 解:由函数图象可得:A=$\sqrt{2}$,周期T=4($\frac{7π}{12}-\frac{π}{3}$)=π,由周期公式可得:$ω=\frac{2π}{π}=2$,
由点($\frac{π}{3}$,0)在函数的图象上,可得:$\sqrt{2}$sin(2×$\frac{π}{3}$+φ)=0,
解得:φ=kπ$-\frac{2π}{3}$,k∈Z,
当k=1时,可得φ=$\frac{π}{3}$,
从而得解析式可为:$f(x)=\sqrt{2}sin({2x+\frac{π}{3}})$.
点评 本题考查的知识点是正弦型函数解析式的求法,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知角D的终边经过点P(-3,4),那么sinα+2cosα的值等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{1}{5}$ |
5.已知三个正实数a,b,c满足b<a+c≤2b,a<b+c≤2a,则$\frac{a}{b}$的取值范围为( )
| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,$\frac{3}{2}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{3}{2}$,2) |