题目内容
9.某科技兴趣小组需制作一个面积为$2\sqrt{2}$平方米,底角为45°的等腰梯形构件,则该梯形构件的周长的最小值为8米.分析 设等腰梯形的上底为y米,高为x米,由底角为45°,则下底为2x+y米,运用梯形的面积公式,可得x+y为x的表达式,再由基本不等式,即可得到周长的最小值.
解答 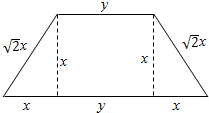 解:设等腰梯形的上底为y米,高为x米,
解:设等腰梯形的上底为y米,高为x米,
由底角为45°,则下底为2x+y米,
则等腰梯形的面积为S=$\frac{1}{2}$x(2x+2y)=2$\sqrt{2}$,
即为x(x+y)=2$\sqrt{2}$,
即有x+y=$\frac{2\sqrt{2}}{x}$,
周长为c=2(x+y)+2$\sqrt{2}$x=$\frac{4\sqrt{2}}{x}$+2$\sqrt{2}$x
≥2$\sqrt{\frac{4\sqrt{2}}{x}•2\sqrt{2}x}$=8.
当且仅当$\frac{4\sqrt{2}}{x}$=2$\sqrt{2}$x,即x=$\sqrt{2}$时,取得最小值,且为8米.
故答案为:8.
点评 本题考查基本不等式在最值应用题中的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.已知△AOB的顶点坐标分别是A(4,0),B(0,3),O(0,0)则△AOB外接圆的方程是( )
| A. | x2+y2+4x-3y=0 | B. | x2+y2-4x-3y=0 | C. | x2+y2+4x+3y=0 | D. | x2+y2-4x+3y=0 |
20.双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$的焦距为( )
| A. | $3\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $4\sqrt{5}$ |
1.已知O是锐角△ABC的外接圆圆心,∠A=30°,$\frac{cosB}{sinC}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$=2m•$\overrightarrow{AO}$,则m的值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
14.已知cos(π-α)=-$\frac{3}{5}$,且α是第一象限角,则sin(-2π-α)的值是( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
 如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3小组的频数为18,则n的值是48.
如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3小组的频数为18,则n的值是48.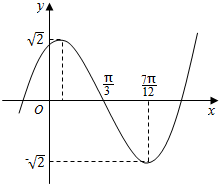 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.