题目内容
20.已知复平面上的正方形的三个顶点对应的复数分别为1+2i,-2+i,-1-2i,那么第四个顶点对应的复数是2-i.分析 根据复数的几何意义以及正方形的性质进行求解即可.
解答 解:不妨设正方形ABCD的三个顶点A,B,C对应的复数分别为1+2i,-2+i,-1-2i,
则A(1,2),B(-2,1),C(-1,-2),
设D(x,y),
则满足$\overrightarrow{AB}=\overrightarrow{DC}$,即(-3,-1)=(-1-x,-2-y)
即$\left\{\begin{array}{l}{-1-x=-3}\\{-2-y=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,
满足$\overrightarrow{AB}•\overrightarrow{BC}=0$
则D(2,-1),对应的复数为2-i,
故答案为:2-i
点评 本题主要考查复数的几何意义,利用复数相等是解决本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
5.如图给出的是计算和式$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
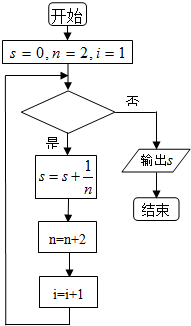

| A. | i≤11 | B. | i≤10 | C. | i≥10 | D. | i≥11 |
12.阅读下图所示的程序框图,该框图表示的函数是( )
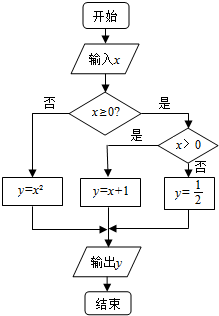

| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
9.命题“若p3+q3=2,则p+q≤2”的结论的否定应该是( )
| A. | p+q=2 | B. | p+q≥2 | C. | p+q≠2 | D. | p+q>2 |
 如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3小组的频数为18,则n的值是48.
如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3小组的频数为18,则n的值是48.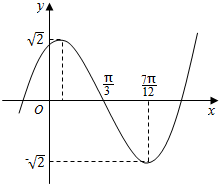 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.