题目内容
5.已知三个正实数a,b,c满足b<a+c≤2b,a<b+c≤2a,则$\frac{a}{b}$的取值范围为( )| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,$\frac{3}{2}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{3}{2}$,2) |
分析 将不等式进行转化,利用不等式的性质建立关于$\frac{b}{a}$的不等式关系,即可得到结论.
解答 解:∵三个正数a,b,c,满足b<a+c≤2b,a<b+c≤2a,
∴$\frac{b}{a}$<1+$\frac{c}{a}$≤$\frac{2b}{a}$,1<$\frac{b}{a}$+$\frac{c}{a}$≤2
即-$\frac{2b}{a}$≤-1-$\frac{c}{a}$<-$\frac{b}{a}$,
不等式的两边同时相加得1-$\frac{2b}{a}$<$\frac{b}{a}$-1<2-$\frac{b}{a}$,
则等价为$\left\{\begin{array}{l}{1-\frac{2b}{a}<\frac{b}{a}-1}\\{\frac{b}{a}-1<2-\frac{b}{a}}\end{array}\right.$,
即$\left\{\begin{array}{l}{\frac{b}{a}>\frac{2}{3}}\\{\frac{b}{a}<\frac{3}{2}}\end{array}\right.$,
即$\frac{2}{3}$<$\frac{b}{a}$<$\frac{3}{2}$,即$\frac{2}{3}$<$\frac{a}{b}$<$\frac{3}{2}$,
即$\frac{a}{b}$的取值范围为($\frac{2}{3}$,$\frac{3}{2}$),
故选:B.
点评 本题主要考查不等式的解法,利用不等式的性质将不等式进行转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=$\sqrt{3}$,A+C=2B,则sinC=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
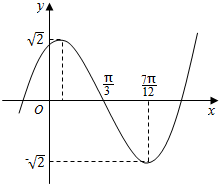 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式. 如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.