题目内容
4.已知角D的终边经过点P(-3,4),那么sinα+2cosα的值等于( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{1}{5}$ |
分析 由条件利用任意角的三角函数的定义求得sinα和cosα的值,可得sinα+2cosα的值.
解答 解:由题意可得,x=-3、y=4、r=|OP|=5,∴sinα=$\frac{y}{r}$=$\frac{4}{5}$,cosα=$\frac{x}{r}$=-$\frac{3}{5}$,
∴sinα+2cosα=$\frac{4}{5}$-$\frac{6}{5}$=-$\frac{2}{5}$,
故选:C.
点评 本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
14.已知cos(π-α)=-$\frac{3}{5}$,且α是第一象限角,则sin(-2π-α)的值是( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12.阅读下图所示的程序框图,该框图表示的函数是( )
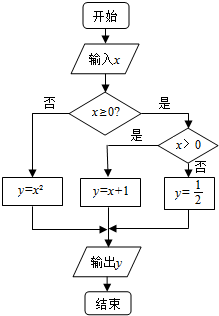

| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
19.100辆汽车通过某一段公路时,时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约有( )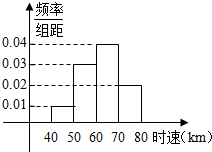

| A. | 60辆 | B. | 80辆 | C. | 70辆 | D. | 140辆 |
9.命题“若p3+q3=2,则p+q≤2”的结论的否定应该是( )
| A. | p+q=2 | B. | p+q≥2 | C. | p+q≠2 | D. | p+q>2 |
14.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=$\sqrt{3}$,A+C=2B,则sinC=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
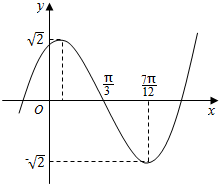 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式. 如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.