题目内容
6.已知f(x)=x2-ax-6a,其中a是常数.(1)若f(x)<0的解集是{x|-3<x<6},求a的值,并解不等式$\frac{f(x)}{x-a}$≥0.
(2)若不等式f(x)<0有解,且解区间长度不超过5个长度单位,求a的取值范围.
分析 (1)由题意可得f(x)=x2-ax-6a<0的解集是{x|-3<x<6},利用韦达定理求得a=3,用穿根法求得不等式$\frac{f(x)}{x-a}≥0$的解集.
(2)设f(x)=x2-ax-6a<0的解集是{x|x1<x<x2},由判别式大于零求得a的范围;由|x2-x1|≤5求得a的范围,再把这2个a的范围取交集,可得所求.
解答 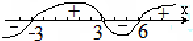 解:(1)∵f(x)=x2-ax-6a<0的解集是{x|-3<x<6},
解:(1)∵f(x)=x2-ax-6a<0的解集是{x|-3<x<6},
∴x2-ax-6a=0的两根是x1=-3,x2=6,
∴x1+x2=a=-3+6,x1•x2=-6a=-3×6,∴a=3,
∴不等式$\frac{f(x)}{x-a}=\frac{{{x^2}-3x-18}}{x-3}≥0$,即 $\frac{{{x^2}-3x-18}}{x-3}=\frac{{({x-6})(x+3)}}{x-3}≥0$,
用穿根法求得不等式$\frac{f(x)}{x-a}≥0$的解集是{x|-3≤x<3或x≥6}.
(2)设f(x)=x2-ax-6a<0的解集是{x|x1<x<x2},
依题意$\left\{{\begin{array}{l}{△={{({-a})}^2}+24a>0}\\{{x_1}+{x_2}=a,{x_1}•{x_2}=-6a}\\{|{{x_2}-{x_1}}|≤5}\end{array}}\right.$.
∴由a2+24a>0,求得a>0或a<-24,
由|x2-x1|≤5得${({x{\;}_1+{x_2}})^2}-4{x_1}{x_2}≤25$,
∴a2+24a-25≤0,∴-25≤a≤1,
∴-25≤a<-24或0<a≤1,∴所求a的取值范围是[-25,-24)∪(0,1].
点评 本题主要考查分式不等式、一元二次不等式的解法,二次函数的性质、韦达定理的应用,属于基础题.

 步步高达标卷系列答案
步步高达标卷系列答案| A. | $3\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $4\sqrt{5}$ |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}-1$ | D. | $\frac{{\sqrt{2}}}{2}$ |
 如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.
如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.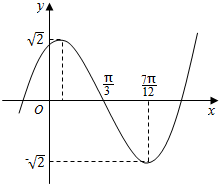 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式. 如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.