题目内容
3.关于x的方程$\frac{1}{sinx}$+$\frac{1}{cosx}$+$\frac{1}{sinxcosx}$-a=0在(0,$\frac{π}{2}$)内有解,则a的取值范围是[2+2$\sqrt{2}$,+∞).分析 由题意可得a=$\frac{sinx+cosx+1}{sinxcosx}$,令sinx+cosx=t∈( 1,$\sqrt{2}$],则sinxcosx=$\frac{{t}^{2}-1}{2}$,a=$\frac{t+1}{\frac{{t}^{2}-1}{2}}$=$\frac{2}{t-1}$,再利用不等式的基本性质求得a的范围.
解答 解:由题意可得a=$\frac{1}{sinx}$+$\frac{1}{cosx}$+$\frac{1}{sinx•cosx}$=$\frac{sinx+cosx+1}{sinxcosx}$,令sinx+cosx=t=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈( 1,$\sqrt{2}$],
则sinxcosx=$\frac{{t}^{2}-1}{2}$,a=$\frac{t+1}{\frac{{t}^{2}-1}{2}}$=$\frac{2}{t-1}$,故当t=$\sqrt{2}$时,a取得最小值为2$\sqrt{2}$+2,当t趋于1时,a趋于无穷大,
故a的范围为[2+2$\sqrt{2}$,+∞),
故答案为:[2+2$\sqrt{2}$,+∞).
点评 本题主要考查正弦函数的定义域和值域,不等式的基本性质,属于基础题.

练习册系列答案
相关题目
14.已知cos(π-α)=-$\frac{3}{5}$,且α是第一象限角,则sin(-2π-α)的值是( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12.阅读下图所示的程序框图,该框图表示的函数是( )
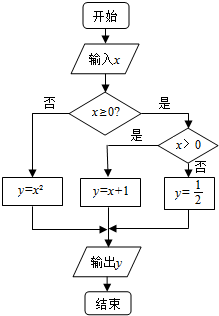

| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
 如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.
如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.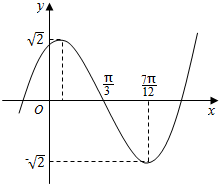 已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.
已知函数f(x)=Asin(wx+φ),(A,w,φ是常数,A>0,w>0)的部分图象如图所示,试求f(x)的解析式.