题目内容
(本小题共12分)
(普通高中做)
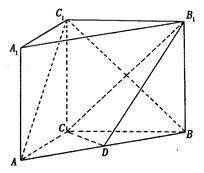
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,点D是AB的中点,
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
(III)求异面直线 AC1与 B1C所成角的余弦值.

解:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,

∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1………4分
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,∴ AC1//平面CDB1;………8分
平面CDB1,∴ AC1//平面CDB1;………8分
(III)∵ DE//AC1,∴∠CED为AC1与B1C所成的角,
在△CED中,ED= AC 1=
AC 1= ,CD=
,CD= AB=
AB= ,CE=
,CE= CB1=2
CB1=2 ,
,
∴ ,
,
∴异面直线AC1与B1C所成角的余弦值 .………12分
.………12分

∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1………4分
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE
 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,∴ AC1//平面CDB1;………8分
平面CDB1,∴ AC1//平面CDB1;………8分(III)∵ DE//AC1,∴∠CED为AC1与B1C所成的角,
在△CED中,ED=
 AC 1=
AC 1= ,CD=
,CD= AB=
AB= ,CE=
,CE= CB1=2
CB1=2 ,
,∴
 ,
,∴异面直线AC1与B1C所成角的余弦值
 .………12分
.………12分
练习册系列答案
相关题目
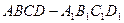 棱长为1,以
棱长为1,以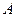 为坐标原点,以直线
为坐标原点,以直线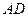 为横轴,直线
为横轴,直线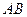 为纵轴,直线
为纵轴,直线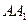 为竖轴建立空间直角坐标系,如图.
为竖轴建立空间直角坐标系,如图. 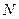 为
为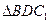 的重心,
的重心,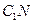
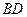 于
于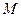 .(I)求点
.(I)求点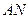 与平面
与平面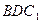 所成的角的大小.
所成的角的大小.
 , 四边形
, 四边形 是梯形,
是梯形, ∥
∥ ,
,  ,
, ,
, 

 中
中 点。
点。
 ∥平面
∥平面 ;
; 所成角的余弦值。
所成角的余弦值。
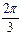 ,直线m⊥M,则平面N内的直线与m所成角的取值范围是
,直线m⊥M,则平面N内的直线与m所成角的取值范围是 



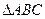 沿DE、EF、DF折成三棱锥P—DEF,如图所示,则异面直线PG与MN所成角的大小为 ▲
沿DE、EF、DF折成三棱锥P—DEF,如图所示,则异面直线PG与MN所成角的大小为 ▲ 
 角
角 角
角 ,B、C两点间的球面距离是
,B、C两点间的球面距离是 ,则二面角
,则二面角 的大小是
的大小是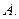





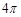 ,A、B、C三点都在球面上,且任意两点间的球面距离为
,A、B、C三点都在球面上,且任意两点间的球面距离为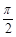 ,则OA与平面ABC所成角的正切值是________________.
,则OA与平面ABC所成角的正切值是________________.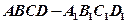 的顶点
的顶点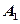 在空间作直线
在空间作直线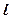 与
与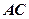 和
和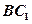 所成的角都等于
所成的角都等于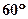 ,则这样的直线
,则这样的直线