Question

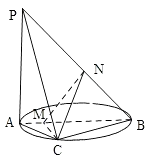
【题目】如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的点．

（1）求证：平面PAC⊥平面PBC；
（2）若AB=2，AC=1，PA=1，求证：二面角C﹣PB﹣A的余弦值．

Answer 1

【答案】
（1）证明：如图，

由AB是圆的直径，得AC⊥BC．

由PA⊥平面ABC，BC平面ABC，得PA⊥BC．

又PA∩AC=A，PA平面APC，AC平面PAC，

所以BC⊥平面PAC．

因为BC平面PBC，

所以平面PAC⊥平面PBC；

（2）解：过C作CM⊥AB于M，

因为PA⊥平面ABC，CM平面ABC，所以PA⊥CM，

故CM⊥平面PAB．

过M作MN⊥PB于N，连接NC．

由三垂线定理得CN⊥PB．

所以∠CNM为二面角C﹣PB﹣A的平面角．

在Rt△ABC中，由AB=2，AC=1，得 ， ， ．

在Rt△ABP中，由AB=2，AP=1，得 ．

因为Rt△BNM∽Rt△BAP，所以 ．

故MN= ．

又在Rt△CNM中， ．故cos ．

所以二面角C﹣PB﹣A的余弦值为 ．

【解析】（1）要证平面PAC⊥平面PBC，只要证明平面PBC经过平面PAC的一条垂线BC即可，利用题目给出的条件借助于线面垂直的判定定理能够证明BC⊥平面PAC（2）因为平面PAB和平面ABC垂直，只要在平面ABC内过C作两面的交线AB的垂线，然后过垂足再作PB的垂线，连结C和后一个垂足即可得到二面角C﹣PB﹣A的平面角，然后在作出的直角三角形中通过解直角三角形即可求得二面角C﹣PB﹣A的余弦值．
【考点精析】通过灵活运用平面与平面垂直的判定，掌握一个平面过另一个平面的垂线，则这两个平面垂直即可以解答此题．