题目内容
19.已知F1,F2为椭圆$\frac{x^2}{4}+\frac{y^2}{9}=1$两个焦点,P为椭圆上一点且|PF1|=1,则|PF2|=( )| A. | 3 | B. | 9 | C. | 4 | D. | 5 |
分析 利用椭圆定义直接计算即可.
解答 解:由题意可知:|PF1|+|PF2|=2a=2$\sqrt{9}$=6,
∴|PF2|=6-|PF1|=6-1=5,
故选:D.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
11.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{\sqrt{41}}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
9.圆x2+y2-2x+4y+3=0的圆心坐标为( )
| A. | (-1,2) | B. | (1,-2) | C. | (-2,4) | D. | (2,-4) |
 如图,在矩形ABCD中,AB=2,AD=1,在平面内将矩形ABCD绕点B按顺时针方向旋转60°后得到矩形A′BC′D′,则点D′到直线AB的距离是$\sqrt{3}+\frac{1}{2}$.
如图,在矩形ABCD中,AB=2,AD=1,在平面内将矩形ABCD绕点B按顺时针方向旋转60°后得到矩形A′BC′D′,则点D′到直线AB的距离是$\sqrt{3}+\frac{1}{2}$.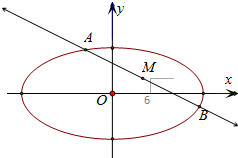 已知过点M (2,1)的直线l和椭圆x2+4y2=36相交于点A、B,且线段AB恰好以M为中点,求直线l的方程和线段AB的长.
已知过点M (2,1)的直线l和椭圆x2+4y2=36相交于点A、B,且线段AB恰好以M为中点,求直线l的方程和线段AB的长.