题目内容
7.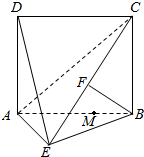 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.(1)求证:平面ADE⊥平面BCE;
(2)求二面角E-AC-B的大小;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
分析 ( 1)根据面面垂直的判定定理推断出平面ADE⊥平面BCE;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角E-AC-B的大小;
(3)在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连MN,证明平面MGE∥平面ADE,可得MN∥平面ADE,从而可得结论.
解答 证明:(Ⅰ)∵BF⊥平面ACE,AE?平面ACE,
∴BF⊥AE,BF⊥CE,
∵EB=BC,∴F是CE的中点,
又∵AD⊥平面ABE,AD?平面ABCD,
∴平面ABCD⊥平面ABE,
∵平面ABCD∩平面ABE=AB,BC⊥AB
∴BC⊥平面ABE,
从而BC⊥AE,且BC∩BF=B,
∴AE⊥平面BCE,
又AE?平面ADE,
故平面平面ADE⊥平面BCE.
(2)由(1)知AE⊥平面BCE,
∴AE⊥BE,即∠AEB=90°,
取AB的中点O,连接OE,
则OE⊥AB,
建立以O为原点,OA,OE,OH为x,y,z轴的空间坐标系如图:
∵AE=EB=BC=2,
∴AB=2√2√2,OA=OE=√2√2,
则A(√2√2,0,0),E(0,√2√2,0),B(-√2√2,0,0),H(O,0,2),C(-√2√2,0,2),
则平面ACB的一个法向量为→m→m=(0,1,0),
设平面EAC的法向量为→n→n=(x,y,z),
则→AC−−→AC=(-2√2√2,0,2),→AE−−→AE=(-√2√2,√2√2,0),
由{→n•→AC=0→n•→AE=0,得{−2√2x+2z=0−√2x+√2y=0,
令x=1,则y=1,z=√2,
即→n=(1,1,√2),
则cos<→m,→n>=→m•→n|→m||→n|=11×√1+1+2=1√4=12,
即<→m,→n>=60°,
故二面角E-AC-B的大小为60°.
(3)在△ABE中过M点作MG∥AE交BE于G点,
在△BEC中过G点作GN∥BC交EC于N点,连MN,
∴CN=13CE.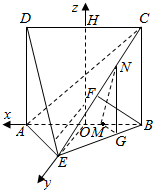
∵MG∥AE,MG?平面ADE,AE?平面ADE,
∴MG∥平面ADE.
同理,GN∥平面ADE,且MG与GN交于G点,
∴平面MGE∥平面ADE.
又MN?平面MGN,
∴MN∥平面ADE.
故N点为线段CE上靠近C点的一个三等分点.
点评 本题考查面面垂直和线面平行的判定,以及二面角的求解,建立空间坐标系,利用向量法是解决二面角的基本方法.

| A. | 34 | B. | 23 | C. | 35 | D. | 1 |
| A. | k=2 | B. | k=-2 | C. | k=12 | D. | k=−12 |
| A. | 720种 | B. | 48种 | C. | 96种 | D. | 192种 |
| A. | 10 | B. | 6 | C. | 5 | D. | 4 |
 如图,在矩形ABCD中,AB=2,AD=1,在平面内将矩形ABCD绕点B按顺时针方向旋转60°后得到矩形A′BC′D′,则点D′到直线AB的距离是
如图,在矩形ABCD中,AB=2,AD=1,在平面内将矩形ABCD绕点B按顺时针方向旋转60°后得到矩形A′BC′D′,则点D′到直线AB的距离是