题目内容
【题目】已知圆O:![]() ,直线l:
,直线l:![]() .
.
(1)若直线l与圆O相切,求k的值;
(2)若直线l与圆O交于不同的两点A,B,当![]() 为锐角时,求k的取值范围;
为锐角时,求k的取值范围;
(3)若![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点,若过定点,则求出该定点.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点,若过定点,则求出该定点.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)直线CD过定点
;(3)直线CD过定点![]() .
.
【解析】
(1)由圆心到切线距离等于半径求参数值;
(2)只要圆心到直线的距离大于弦长的一半即可.
(3)利用![]() 点坐标,求出直线
点坐标,求出直线![]() 的方程,由方程确定是否过定点.
的方程,由方程确定是否过定点.
(1)原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,由
,由![]() ,解得
,解得![]() ;
;
(2)因为![]() ,
,![]() 为锐角时等价于
为锐角时等价于![]() ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() ;
;
(3)![]() 在直线
在直线![]() 上,设
上,设![]() ,则以
,则以![]() 为直径的圆方程为
为直径的圆方程为![]() ,即
,即![]() ,
,
同 ,相减得
,相减得![]() ,这就是直线
,这就是直线![]() 的方程.
的方程.
又![]() ,
,
∴![]() ,
,![]() ,由
,由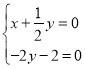 得
得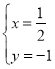 ,
,
∴直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目



