题目内容
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别为
分别为![]() 的中点.有下述四个结论:①直线
的中点.有下述四个结论:①直线![]() 与直线
与直线![]() 垂直;②直线
垂直;②直线![]() 与平面
与平面![]() 平行;③平面
平行;③平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() ;④直线
;④直线![]() 与直线
与直线![]() 所成角的正切值为
所成角的正切值为![]() ;其中所有正确结论的编号是( )
;其中所有正确结论的编号是( )

A.②③B.②④C.①③D.③④
【答案】A
【解析】
①利用线线平行,将![]() 与
与![]() 的位置关系转换为判断
的位置关系转换为判断![]() 与
与![]() 的位置关系;②作出辅助线:取
的位置关系;②作出辅助线:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,然后利用面面平行判断;③作出截面,再根据梯形的面积公式求需要的线段长;④利用平移的思想,将两条异面直线平移在同一个平面内,然后结合余弦定理求夹角的余弦值,再转化为正切值.
,然后利用面面平行判断;③作出截面,再根据梯形的面积公式求需要的线段长;④利用平移的思想,将两条异面直线平移在同一个平面内,然后结合余弦定理求夹角的余弦值,再转化为正切值.
对于①,因为![]() ,若
,若![]() ,则
,则![]() ,从图中可以看出,
,从图中可以看出,
![]() 与
与![]() 相交,但不垂直,所以①错误;
相交,但不垂直,所以①错误;
对于②,如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则有
,则有![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,即②正确;
,即②正确;

对于③,如图所示,连接![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,
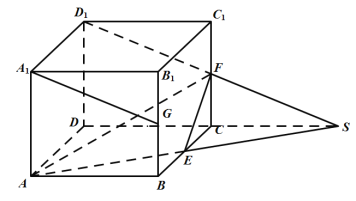
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,所以截面即为梯形
四点共面,所以截面即为梯形![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() 即
即![]() ,
,![]() ,
,
所以等腰△![]() 的高
的高![]() ,梯形
,梯形![]() 的高为
的高为![]() ,
,
所以梯形![]() 的面积为
的面积为![]() ,所以③正确;
,所以③正确;
对于④,因为![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 所成角即为所求.
所成角即为所求.
在三角形![]() 中,
中,![]() ,由余弦定理得,
,由余弦定理得, ,
,
因为直线的夹角范围为![]() ,
,![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 所成角的正切值为3.所以④错误.
所成角的正切值为3.所以④错误.
故选:![]() .
.

【题目】现代社会对破译密码的难度要求越来越高,有一处密码把英文的明文(真实名)按字母分解,其中英文a,b,c……,z这26个字母,依次对应1,2,3……,26这26个正整数.(见下表)
a | b | c | d | e | f | g | h | i | j | k | l | m |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
n | o | p | q | r | s | t | u | v | w | x | y | z |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
用如下变换公式: 将明文转换成密码.如
将明文转换成密码.如![]() .即h变成q;再如:
.即h变成q;再如:![]() ,即y变成m;按上述变换规则,若将明文译成的密码是gano,那么原来的明文是______________.
,即y变成m;按上述变换规则,若将明文译成的密码是gano,那么原来的明文是______________.