题目内容
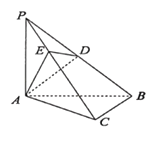
【题目】已知点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点,![]() ,
,![]() ,
,
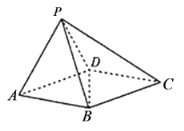
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)因为![]() 是菱形,可得
是菱形,可得![]() ,进而证明
,进而证明![]() ,在由勾股定可证明
,在由勾股定可证明![]() ,根据线面垂直的判定定理可证
,根据线面垂直的判定定理可证![]() 平面
平面![]() ,再根据面面垂直的判定定理,即可证明结果;
,再根据面面垂直的判定定理,即可证明结果;
(2)根据题意建立空间直角坐标系![]() ,再利用空间向量的坐标运算公式求出二面角
,再利用空间向量的坐标运算公式求出二面角![]() 的余弦值.
的余弦值.
(1)证明:设![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,
∵![]() 是菱形,
是菱形,![]()
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
又![]()
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ;
;
(2)由(1)得![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 的方向为
的方向为![]() 轴的正方向,建立如图的空间直角坐标系
轴的正方向,建立如图的空间直角坐标系![]() ,则
,则![]()
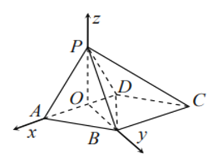
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则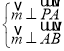 ,∴
,∴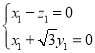
令![]() ,则
,则![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则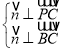 ,∴
,∴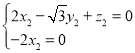 ,
,
令![]() ,则
,则![]() ,
,
∴
又二面角![]() 为钝二面角,
为钝二面角,
∴二面角![]() 的余弦值
的余弦值![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】“读书可以让人保持思想活跃,让人得到智慧启发,让人滋养浩然之气”,2018年第一期中国青年阅读指数数据显示,从供给的角度,文学阅读域是最多的,远远超过了其他阅读域的供给量.某校采用分层抽样的方法从1000名文科生和2000名理科生中抽取300名学生进行了在暑假阅读内容和阅读时间方面的调查,得到数据如表:
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 130 | ||
文科生 | 45 | ||
合计 |
(1)先完成上面的表格,并判断能否有90%的把握认为学生所学文理与阅读内容有关?
(2从300名被调查的学生中,随机进取30名学生,整理其日平均阅读时间(单位:分钟)如表:
阅读时间 |
|
|
|
|
|
男生人数 | 2 | 4 | 3 | 5 | 2 |
女生人数 | 1 | 3 | 4 | 3 | 3 |
试估计这30名学生日阅读时间的平均值(同一组中的数据以这组数据所在区间中点的值作代表)
(3)从(2)中日均阅读时间不低于120分钟的学生中随机选取2人介绍阅读心得,求这两人都是女生的概率.
参考公式: 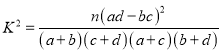 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |