题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中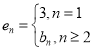 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
【答案】(I)详见解析;(II)![]() ;(III)
;(III)![]() 为指数型和.
为指数型和.
【解析】
(I)通过计算证明证得![]() ,来证得数列
,来证得数列![]() 是等比数列.
是等比数列.
(II)利用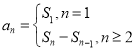 求得数列
求得数列![]() 的通项公式,由
的通项公式,由![]() ,
,![]() ,求得
,求得![]() 的最小值.
的最小值.
(III)先求得![]() 的通项公式,对
的通项公式,对![]() 分成偶数和奇数两种情况进行分类讨论,根据“指数型和”的定义,求出符合题意的“指数型和”.
分成偶数和奇数两种情况进行分类讨论,根据“指数型和”的定义,求出符合题意的“指数型和”.
(I)![]() ,
,![]() .由于
.由于![]() ,当
,当![]() 时,
时,![]() ,所以数列
,所以数列![]() 是等比数列.
是等比数列.![]() ,
,![]() .
.
(II)由(I)得![]() ,
,![]()
![]() ,所以
,所以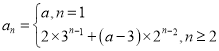 .因为
.因为![]() ,
,![]() .当
.当![]() 时,
时,
![]() ,
,![]() ,而
,而![]() ,所以
,所以![]() ,即
,即![]()
![]() ,化简得
,化简得![]() ,由于当
,由于当![]() 时,
时,![]() 单调递减,最大值为
单调递减,最大值为![]() ,所以
,所以
![]() ,又
,又![]() ,所以
,所以![]() 的最小值为
的最小值为![]() .
.
(III)由(I)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.![]() 也符合上式,所以对正整数
也符合上式,所以对正整数![]() 都有
都有![]() .由
.由![]() ,(
,(![]() 且
且![]() ),
),![]() 只能是不小于
只能是不小于![]() 的奇数.
的奇数.
①当![]() 为偶数时,
为偶数时,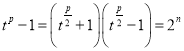 ,由于
,由于![]() 和
和![]() 都是大于
都是大于![]() 的正整数,所以存在正整数
的正整数,所以存在正整数![]() ,使得
,使得![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,相应的
,相应的![]() ,即有
,即有![]() ,
,![]() 为“指数型和”;
为“指数型和”;
② 当![]() 为奇数时,
为奇数时,![]() ,由于
,由于![]() 是
是![]() 个奇数之和,仍为奇数,又
个奇数之和,仍为奇数,又![]() 为正偶数,所以
为正偶数,所以![]() 不成立,此时没“指数型和”.
不成立,此时没“指数型和”.
综上所述,![]() 中的项存在“指数型和”,为
中的项存在“指数型和”,为![]() .
.

练习册系列答案
相关题目
【题目】2019年高考刚过,为了解考生对全国2卷数学试卷难度的评价,随机抽取了某学校50名男考生与50名女考生,得到下面的列联表:
非常困难 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分别估计该学校男考生、女考生觉得全国2卷数学试卷非常困难的概率;
(2)从该学校随机抽取3名男考生,2名女考生,求恰有4名考生觉得全国2卷数学试卷非常困难的概率.