Question

【题目】在平面直角坐标系xOy内，点（）在椭圆E：（a＞0，b＞0），椭圆E的离心率为，直线l过左焦点F且与椭圆E交于A、B两点

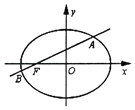
（1）求椭圆E的标准方程；

（2）若动直线l与x轴不重合，在x轴上是否存在定点P，使得PF始终平分∠APB？若存在，请求出点P的坐标：若不存在，请说明理由.

Answer 1

【答案】（1）1；（2）存在，P（﹣4，0）

【解析】

（1）根据，a2＝b2+c2和点（）在椭圆E上，可得；（2）假设存在定点P（t，0）满足题意，设直线l的方程x＝my﹣2，A（x，y），B（x'，y'），

（1）由题意得：e，a，1，且a2＝b2+c2，解得：a2＝8，b2＝4，

所以椭圆E的方程：1；

（2）假设存在定点P（t，0）满足题意，由（1）得左焦点F（﹣2，0），

设直线l的方程：x＝my﹣2，A（x，y），B（x'，y'），

联立与椭圆的方程整理得：（2+m2）y2﹣4my﹣4＝0，

∴y+y'，yy'，

PF始终平分∠APB知：kAP+kBP＝0，

所以kAP+kBP0，

又x＝my﹣2，x'＝my'﹣2，

∴2myy'﹣（t+2）（y+y'）＝0，

即2m（t+2）0，

即（t+4）m＝0，

∴t＝﹣4，

所以存在定点P（﹣4，0）满足题意