设i是虚数单位.复数z1.z2在复平面内的对应点关于实轴对称.z1=1-i.则$\frac{{z} {1}}{{z} {2}}$=( )A．2B．1+iC．iD．-i 题目和参考答案——青夏教育精英家教网—

题目内容

12．设i是虚数单位，复数z₁，z₂在复平面内的对应点关于实轴对称，z₁=1-i，则$\frac{{z}_{1}}{{z}_{2}}$=（　　）

A．

B．

1+i

C．

D．

-i

分析由对称性可得z₂=1+i，代入要求的式子化简即可．

解答解：∵复数z₁，z₂在复平面内的对应点关于实轴对称且z₁=1-i，
∴由对称性可得z₂=1+i，
∴$\frac{{z}_{1}}{{z}_{2}}$=$\frac{1-i}{1+i}$=$\frac{（1-i）^{2}}{（1+i）（1-i）}$=$\frac{-2i}{2}$=-i
故选：D

点评本题考查复数的代数形式的乘除运算，涉及复数的几何意义，属基础题．

练习册系列答案

相关题目

2．

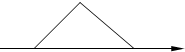用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形（如图所示，其中的x轴表示水平方向），斜边长为2，则原三角形的面积为（　　）

3．已知实数a，b，c，满足0＜a≤b≤c≤$\frac{1}{2}$，求证：$\frac{2}{c（1-c）}$≤$\frac{1}{a（1-b）}$+$\frac{1}{b（1-a）}$．

20．双曲线x²-y²=2的实轴长为2$\sqrt{2}$，离心率为$\sqrt{2}$，渐近线方程为y=±x．

7．已知△ABC中，内角A，B，C的对边分别为a，b，c，若$\overrightarrow{m}$=（b+a，-c），$\overrightarrow{n}$=（b-a，a+c），且$\overrightarrow m⊥\overrightarrow n$；
（1）求角B的值；
（2）若a=6，b=6$\sqrt{3}$，求△ABC的面积．

17．已知△ABC中，点A（-1，0），B（1，0），动点C满足|CA|+|CB|=λ|AB|（常数λ＞1），C点的轨迹为Γ．
（Ⅰ）试求曲线Γ的轨迹方程；
（Ⅱ）当λ=$\sqrt{3}$时，过定点B（1，0）的直线与曲线Γ相交于P，Q两点，N是曲线Γ上不同于P，Q的动点，试求△NPQ面积的最大值．

4．（x-2y）⁷的展开式中的第4项为（　　）

-35x⁴y³

280x⁴y³

-280x⁴y³

35x⁴y³

1．从装有红球、黑球和白球的口袋中摸出一个球，若摸出的球是红球的概率是0.4，摸出的球是黑球的概率是0.25，那么摸出的球是白球或黑球的概率是（　　）

2．命题“?x∈（-∞，0），使得3^x＜4^x”的否定是?x∈（-∞，0），都有3^x≥4^x．

试题分类