题目内容
【题目】已知函数 
（1）判断f（x）的奇偶性并证明；
（2）若f（x）的定义域为[α，β]（β＞α＞0），判断f（x）在定义域上的增减性，并加以证明；
（3）若0＜m＜1，使f（x）的值域为[logmm（β﹣1），logmm（α﹣1）]的定义域区间[α，β]（β＞α＞0）是否存在？若存在，求出[α，β]，若不存在，请说明理由．
【答案】
（1）解：由 
得f（x）的定义域为（﹣∞，﹣3）∪（3，+∞），关于原点对称．
∵ 
∴f（x）为奇函数
（2）解：∵f（x）的定义域为[α，β]（β＞α＞0），则[α，β]（3，+∞）．
设x1，x2∈[α，β]，则x1＜x2，且x1，x2＞3，
f（x1）﹣f（x2）= 
= 
∵（x1﹣3）（x2+3）﹣（x1+3）（x2﹣3）=6（x1﹣x2）＜0，
∴（x1﹣3）（x2+3）＜（x1+3）（x2﹣3）
即 
，
∴当0＜m＜1时，logm 
，即f（x1）＞f（x2）；
当m＞1时，logm ，即f（x1）＜f（x2），
故当0＜m＜1时，f（x）为减函数；m＞1时，f（x）为增函数．
（3）解：由（1）得，当0＜m＜1时，f（x）在[α，β]为递减函数，
∴若存在定义域[α，β]（β＞α＞0），使值域为[logmm（β﹣1），logmm（α﹣1）]，
则有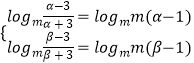 
∴ 
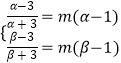
∴α，β是方程 
的两个解
解得当 
时，[α，β]= 
，
当 
时，方程组无解，即[α，β]不存在．
【解析】（1）先求得f（x）的定义域为（﹣∞，﹣3）∪（3，+∞），关于原点对称．再验证 
，从而可得f（x）为奇函数；（2）f（x）的定义域为[α，β]（β＞α＞0），则[α，β]（3，+∞）．设x1 ， x2∈[α，β]，则x1＜x2 ， 且x1 ， x2＞3，作差f（x1）﹣f（x2）= = ，从而可知当0＜m＜1时，logm ，即f（x1）＞f（x2）；当m＞1时，logm 
，即f（x1）＜f（x2），故当0＜m＜1时，f（x）为减函数；m＞1时，f（x）为增函数．（3）由（1）得，当0＜m＜1时，f（x）在[α，β]为递减函数，故若存在定义域[α，β]（β＞α＞0），使值域为[logmm（β﹣1），logmm（α﹣1）]，则有 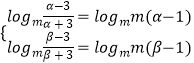，从而问题可转化为α，β是方程 的两个解，进而问题得解．
