Question

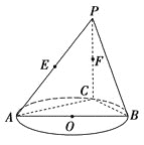
【题目】如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．

(1)记平面BEF与平面ABC的交线为l，试判断直线l与平面PAC的位置关系，并加以证明；

(2)设AB=PC=2,BC=1,求三棱锥P-BEF的体积.

Answer 1

【答案】（1）证明见解析；（2）

【解析】试题分析：（I）直线l∥平面PAC．连接EF，利用三角形的中位线定理可得，EF∥AC；利用线面平行的判定定理即可得到EF∥平面ABC．由线面平行的性质定理可得EF∥l．再利用线面平行的判定定理即可证明直线l∥平面PAC．（II）利用等积法求体积.

试题解析：

解　(1)直线l∥平面PAC.证明如下：

连接EF，因为E，F分别是PA，PC的中点，所以EF∥AC.

又EF平面ABC，且AC平面ABC，所以EF∥平面ABC.

而EF平面BEF，且平面BEF∩平面ABC＝l，所以EF∥l.因为l平面PAC，EF平面PAC，所以直线l∥平面PAC.

(2).