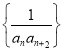题目内容
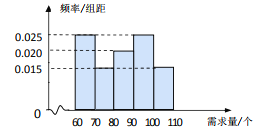
【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以![]() (个)(其中
(个)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)根据直方图计算需求量的中位数;
(2)估计利润![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的数学期望.
的数学期望.
【答案】(1)85个;(2) ![]() ;(3)142.
;(3)142.
【解析】试题分析:(1)需求量的中位数![]() (个)
(个)
(2)由题意可得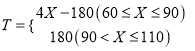 .
.
设利润![]() 不少于100元为事件
不少于100元为事件![]() ,利润
,利润![]() 不少于100元时, 可得
不少于100元时, 可得![]() ,即
,即![]() ,由直方图可知,由此可估计当
,由直方图可知,由此可估计当![]() 时的概率.
时的概率.
(3)由题意,可得利润![]() 的取值可为:80,120,160,180,分别求得
的取值可为:80,120,160,180,分别求得
![]() ,得到利润
,得到利润![]() 的分布列,则
的分布列,则![]() 的数学期望可求.
的数学期望可求.
试题解析:(1)需求量的中位数![]() (个)(其它解法也给分)
(个)(其它解法也给分)
(2)由题意,当![]() 时,利润
时,利润![]() ,
,
当![]() 时,利润
时,利润![]() ,
,
即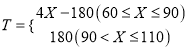 .
.
设利润![]() 不少于100元为事件
不少于100元为事件![]() ,利润
,利润![]() 不少于100元时,即
不少于100元时,即![]() ,
,
∴![]() ,即
,即![]() ,由直方图可知,当
,由直方图可知,当![]() 时,
时,
所求概率: ![]()
(3)由题意,由于![]() ,
,
故利润![]() 的取值可为:80,120,160,180,
的取值可为:80,120,160,180,
且![]() ,
,
故得分布列为:
![]()
利润的数学期望![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人,若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(1)求表格中的数据![]() ;
;
(2)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.