题目内容
设抛物线C的方程y2=4x，O为坐标原点，P为抛物线的准线与其对称轴的交点，过焦点F且垂直于x轴的直线交抛物线于M，N两点，若直线PM与ON相交于点Q，则cos∠MQN=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
练习册系列答案
相关题目
已知命题p：a=1是?x＞0，x+
≥2的充要条件：命题q：?x∈R，x2-x+1＜0．则下列结论中正确的是（ ）
| a |
| x |
| A、p∧q为真命题 |
| B、p∧￢q为真命题 |
| C、￢p∧q为真命题 |
| D、￢p∧￢q为真命题 |
设平面α与平面β相交于直线l，直线a?α，直线b?β，b∥l，则“a∥β”是“a∥b”的（ ）
| A、充分而不必要条件 | B、必要而不充分条件 | C、充要条件 | D、既不充分又不必要条件 |
已知曲线C1：
+y2=1和C2：x2-y2=1的焦点分别为F1、F2，点M是C1和C2的一个交点，则△MF1F2的形状是（ ）
| x2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
已知抛物线C：y=2x2的焦点为F，准线为l，以F为圆心，且与l相切的圆与抛物线C相交于A，B，则|AB|=（ ）
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知两点A（1，-2），B（-4，-2），以下列四条曲线：
①4x+2y=3；
②x2+y2=3；
③x2+2y2=3；
④x2-2y2=3．
其中存在点P，使|PA|=|PB|的曲线有（ ）
①4x+2y=3；
②x2+y2=3；
③x2+2y2=3；
④x2-2y2=3．
其中存在点P，使|PA|=|PB|的曲线有（ ）
| A、①③ | B、②④ | C、①②③ | D、②③④ |
已知函数f（x）=（x+a）2-7lnx+1在（1，+∞）上单调递增，则实数a的取值范围为（ ）
A、（
| ||
B、[
| ||
C、（-∞，
| ||
D、（-∞，-
|
调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据表：
你认为婴儿的性别与出生时间有关系的把握为（ ）
| 晚上 | 白天 | 合计 | |
| 男婴 | 24 | 30 | 54 |
| 女婴 | 8 | 26 | 34 |
| 合计 | 32 | 56 | 88 |
| A、80% | B、90% |
| C、95% | D、99% |
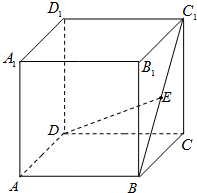如图，在正方体ABCD-A1B1C1D1中，E为BC1的中点，则DE与面BCC1B1所成角的正切值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|