题目内容
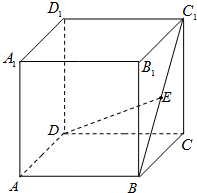 如图,在正方体ABCD-A1B1C1D1中,E为BC1的中点,则DE与面BCC1B1所成角的正切值为( )
如图,在正方体ABCD-A1B1C1D1中,E为BC1的中点,则DE与面BCC1B1所成角的正切值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,建立空直角坐标系,利用向量法能求出DE与面BCC1B1所成角的正切值.
解答:解: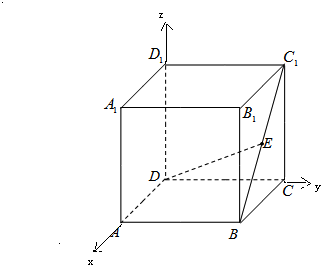 设正方体ABCD-A1B1C1D1的棱长为2,
设正方体ABCD-A1B1C1D1的棱长为2,
以D为原点,以DA为x轴,以DC为y轴,
以DD1为z轴,建立空直角坐标系,
∵E为BC1的中点,
∴D(0,0,0),E(1,2,1),
∴
=(1,2,1),
设DE与面BCC1B1所成角的平面角为θ,
∵面BCC1B1的法向量
=(0,1,0),
∴sinθ=|cos<
,
>|=|
|=
,
∴cosθ=
=
,
∴tanθ=
=
.
故选:C.
 设正方体ABCD-A1B1C1D1的棱长为2,
设正方体ABCD-A1B1C1D1的棱长为2,以D为原点,以DA为x轴,以DC为y轴,
以DD1为z轴,建立空直角坐标系,
∵E为BC1的中点,
∴D(0,0,0),E(1,2,1),
∴
| DE |
设DE与面BCC1B1所成角的平面角为θ,
∵面BCC1B1的法向量
| n |
∴sinθ=|cos<
| DE |
| n |
| 2 | ||
|
| ||
| 3 |
∴cosθ=
1-
|
| ||
| 3 |
∴tanθ=
| ||||
|
| 2 |
故选:C.
点评:本题考查直线与平面所成角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设抛物线C的方程y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M,N两点,若直线PM与ON相交于点Q,则cos∠MQN=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
i为虚数单位,复数z=1+i的模为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
在航天员进行的一项太空实验中,先后要实施6个程序,其中程序B和C都不与D相邻,则实验顺序的编排方法共有( )
| A、216种 | B、288种 | C、180种 | D、144种 |
(1-2x)6的展开式中x2项的系数是( )
| A、12 | B、54 | C、60 | D、160 |
下列四边形中,四个顶点一定在同一个圆上的是( )
| A、平行四边行 | B、菱形 | C、矩形 | D、直角梯形 |
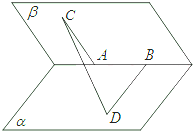 如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=2,AC=3,BD=4,求CD的长.
如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=2,AC=3,BD=4,求CD的长.