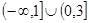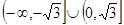题目内容
(本小题满分12分)
设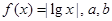 为实数,且
为实数,且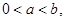
(1)求方程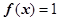 的解;
的解;
(2)若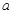 ,
,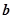 满足
满足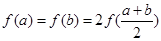 ,试写出
,试写出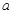 与
与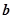 的等量关系(至少写出两个);
的等量关系(至少写出两个);
(3)在(2)的基础上,证明在这一关系中存在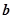 满足
满足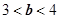 .
.
设
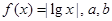 为实数,且
为实数,且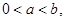
(1)求方程
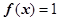 的解;
的解;(2)若
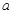 ,
,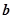 满足
满足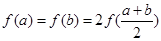 ,试写出
,试写出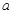 与
与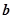 的等量关系(至少写出两个);
的等量关系(至少写出两个);(3)在(2)的基础上,证明在这一关系中存在
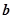 满足
满足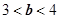 .
.(1)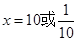 ;(2)
;(2)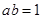 ,
,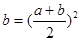 ;
;
(3)方程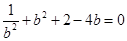 存在
存在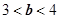 的根.
的根.
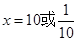 ;(2)
;(2)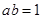 ,
,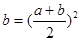 ;
;(3)方程
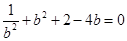 存在
存在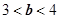 的根.
的根.试题分析:(1)由
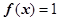 得,
得,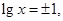 所以
所以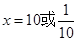
(2)结合函数图像,由
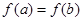 可判断
可判断 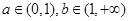 ,
,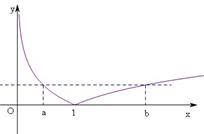
从而
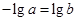 ,从而
,从而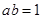
又
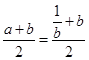 ,
,因为
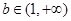 ,所以
,所以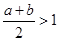
从而由
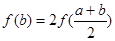
可得
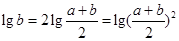 ,
,从而
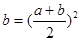
(3)由
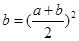
得
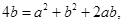
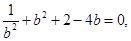 令
令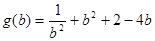 ,
,因为
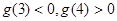 ,根据零点存在性定理可知,
,根据零点存在性定理可知,函数
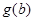 在
在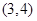 内一定存在零点,
内一定存在零点,即方程
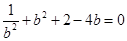 存在
存在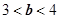 的根.
的根.点评:典型题,对数函数是重要函数之一,因此,对对数函数的图象和性质的考查较为多见。本题将对数函数与函数零点问题结合在一起进行考查,体现了考查到灵活性。(2)小题是一道开放性题目,颇具新意。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
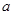 和
和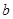 ,定义运算“
,定义运算“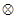 ”:
”: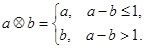 .设函数
.设函数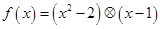 ,
,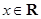 .若函数
.若函数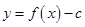 的图象与
的图象与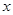 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数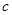 的取值范围是( )
的取值范围是( )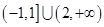
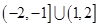
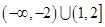
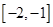

 的单调区间和值域。
的单调区间和值域。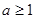 ,求函数
,求函数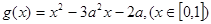 ,若对于任意
,若对于任意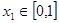 ,总存在
,总存在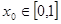 ,使得
,使得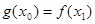 成立,求实数
成立,求实数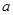 的取值范围。
的取值范围。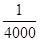 ).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=
).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=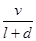 最大?
最大?
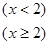 则
则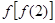 =( )
=( )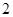
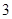
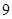
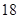
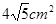 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽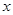 及长
及长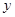 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.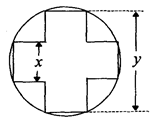
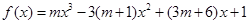 其中
其中
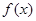 的单调增区间是(0.1),求m的值
的单调增区间是(0.1),求m的值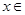
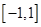 时,函数
时,函数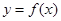 的图像上任意一点的切线斜率恒大于3m,求m的取值范围.
的图像上任意一点的切线斜率恒大于3m,求m的取值范围.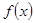 在
在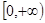 上是增函数,
上是增函数, 若
若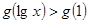 ,则
,则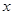 的取值范围是( )
的取值范围是( )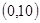
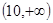

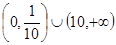
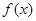 满足
满足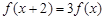 ,当
,当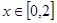 时,
时,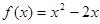 ,若
,若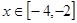 时,
时,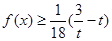 恒成立,则实数
恒成立,则实数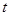 的取值范围是 .
的取值范围是 .