题目内容
1.已知a1=$\frac{1}{2}$,an+1=$\frac{3{a}_{n}}{{a}_{n}+3}$,猜想an=$\frac{3}{n+5}$.分析 通过计算出前几项的值可知分子均为3、分母成公差为1的等差数列,进而可得结论.
解答 解:∵a1=$\frac{1}{2}$,an+1=$\frac{3{a}_{n}}{{a}_{n}+3}$,
∴a2=$\frac{3{a}_{1}}{{a}_{1}+3}$=$\frac{3•\frac{1}{2}}{\frac{1}{2}+3}$=$\frac{3}{7}$,
a3=$\frac{3{a}_{2}}{{a}_{2}+3}$=$\frac{3•\frac{3}{7}}{\frac{3}{7}+3}$=$\frac{3}{8}$,
a4=$\frac{3{a}_{3}}{{a}_{3}+3}$=$\frac{3•\frac{3}{8}}{\frac{3}{8}+3}$=$\frac{3}{9}$,
a5=$\frac{3{a}_{4}}{{a}_{4}+3}$=$\frac{3•\frac{1}{3}}{\frac{1}{3}+3}$=$\frac{3}{10}$,
a6=$\frac{3{a}_{5}}{{a}_{5}+3}$=$\frac{3•\frac{3}{10}}{\frac{3}{10}+3}$=$\frac{3}{11}$,
猜测:an=$\frac{3}{n+5}$,
故答案为:$\frac{3}{n+5}$.
点评 本题考查数列的通项,找出规律是解决本题的关键,注意解题方法的积累,属于中档题.注:本题还可以通过取倒数、构造等差数列{$\frac{1}{{a}_{n}}$}来计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.数列{an}是公比为q的等比数列,若ak=m,则ak+1=( )
| A. | mqk+l-1 | B. | mql | C. | mql-1 | D. | mql+1 |
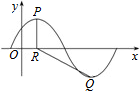 已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$
已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$