题目内容
17.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,求出底面面积,代入锥体体积公式,可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,
其底面面积S=$\frac{1}{2}$×1×(1+1)=1,
高h=$\sqrt{3}$,
故体积V=$\frac{1}{3}Sh$=$\frac{\sqrt{3}}{3}$,
故选:A
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
9.“a+b>0”是“任意的x∈[0,1],ax+b>0恒成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
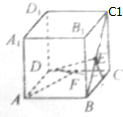 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.